A STUDY OF STRESS CONCENTRATION IN MULTILINK PLATES BY THE METHOD OF BOUNDARY EQUATIONS
A STUDY OF STRESS CONCENTRATION IN MULTILINK PLATES BY THE METHOD OF BOUNDARY EQUATIONS
Abstract
A mathematical model for analysing the stress-strain state of a multilink area based on the method of boundary integral equations is presented. The obtained boundary equations allow to study plane problems of elasticity theory under various influences. As a result of spline approximation of boundary parameters, the system of boundary integral equations is transformed into a system of algebraic equations, where the unknowns are components of displacements and stresses on the contour of the studied object. An elastic isotropic two-dimensional body with an internal area limited by a contour is examined. It is assumed that stresses can be given on one part of the boundary and displacements on the other part. The solution of two-dimensional problems in stresses is reduced to the integration of differential equations of equilibrium. The proposed algorithm is implemented on the example of a two-linked area.
1. Введение
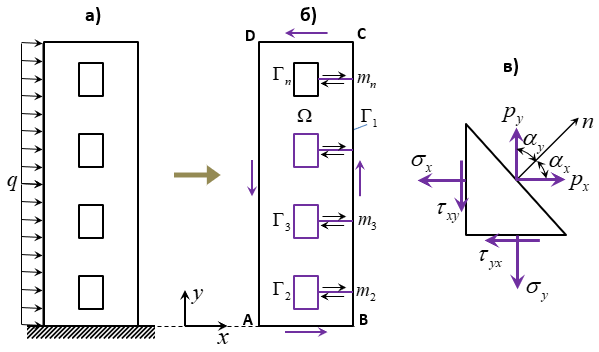
Рисунок 1 - Многосвязная область
2. Дифференциальные уравнения равновесия
Рассмотрим упругое изотропное двумерное тело с внутренней областью Ω, ограниченной контуром Г. Предполагается, что на одной части границы могут быть заданы напряжения, а на другую – перемещения. Решение двумерных задач в напряжениях сводится к интегрированию дифференциальных уравнений равновесия
вместе с условием совместности
и граничными условиями (рис. 1, в)
Здесь: γx, γy – компоненты объемной силы; ν0 = (1+ν) – в случае плоского напряженного состояния; ν0 = 1/(1-ν) – в случае плоской деформации; ν – коэффициент Пуассона; nx = cosαx, ny = cosαy – направляющие косинусы нормали к границе; αx, αy – углы между нормалью и осями x и y соответственно; px, py – заданные на поверхности тело нагрузки (напряжения).
Система из трех уравнений (1) и (2) с тремя неизвестными напряжениями σx, σy и τxy, с учетом граничных условий (3), позволяет определять напряженное состояние двумерной конструкции от заданной нагрузки на контуре Г и объемные силы, заданные внутри области Ω. В случае, когда объемные силы γx и γy постоянны, правая часть в (2) обратится в ноль, то можно заметить, что распределение напряжений в плоской задаче не зависит от свойств материала. Следовательно, уравнения (1) и (2), при γx,γy = const, могут применяться как при упругой, так и неупругой работе материала конструкции. Когда учитываются только силы тяжести, где γx = 0, γy = -ρg = -γ0, ρ – плотность материала, g – ускорение свободного падения, γ0 – объемный вес, решение плоской задачи упрощается введением новой функции φ(x,y) (функция Эри), которая связана с компонентами напряжения зависимостями
Видно, что выражения (4) удовлетворяют уравнения (1) при любых значениях функции φ(x,y), но действительным решением задачи будет то, которое удовлетворяет также уравнению совместности (2), представленное в виде
Подставив (4) в (5), получаем
Таким образом, решение двумерной задачи в напряжениях, когда объемной силой является вес тела, сводится к рассмотрению (6) с учетом граничных условий (3). Бигармоническое уравнение (6) представляет собой условие совместности деформаций, записанное через функцию напряжений φ(x,y). В общем, из решения (6) определяется φ(x,y), а затем поле напряжений вычисляются по формулам (4).
Если учесть, что любую бигармоническую функцию можно представить с помощью аналитических функций комплексного переменного , то становится возможным комплексное представление решений плоской задачи теории упругости. Заменив переменные x, y сопряженными комплексными переменными
бигармоническое уравнение (1.6) можно представить в виде
которое имеет решение
где ϕ(z), ψ(z) – аналитические функции, ϕ ̄(z ̄), ψ ̄(z ̄) – функции, сопряженные с функциями ϕ(z) и ψ(z). Комплексное представление перемещений и напряжений осуществляется по формулам
где ω = 3-4v, v – коэффициент Пуассона. В случае плоского напряженного состояния величину ω следует заменить на ω = (3-v)/(1+v), χ(z)=ψ'(z). Следовательно, решение задачи при заданных внешних напряжениях (1.3), приложенных на границе Г, сводится к отысканию в области Ω двух аналитических функций ϕ(z), ψ(z), связанных граничными условиями. Методы теории функций комплексного переменного, основанные на интегралах типа Коши и конформного преобразования, нашли применение в задачах механики сплошной среды благодаря фундаментальным работам Г.В. Колосова, Н. И. Мусхелишвили, Л.Д. Галина, И.Н. Векуа, И.Н. Снеддон и др.
Если принять за основные неизвестные функции перемещения ux (x,y) и uy (x,y), то заменяя в дифференциальных уравнениях (1.1) компоненты напряжений через компоненты деформаций согласно обобщенному закону Гука, а затем с использованием геометрических уравнений Коши, представляя компоненты деформаций через компоненты перемещений, получаем систему дифференциальных уравнений в перемещениях (уравнения Ламе), которая в условиях плоской деформации записывается в виде ,
где G1=2G(1-ν)/(1-2ν), G2=G/(1-2ν), G – модуль упругости при сдвиге. Заменив в (11) коэффициент Пуассона ν на ν/(1+v), получаем уравнения, соответствующие плоскому напряженному состоянию
здесь G1*=2G(1-ν), G2*=G(1+ν)/(1-ν). Следует отметить, что здесь нет необходимости в использования уравнении совместности деформаций (2), так как мы имеем два уравнения с двумя неизвестными ux (x,y) и uy (x,y).
В данной работе уравнения (11) и (12) будут использованы для составления граничных интегральных уравнений. Система уравнений (11) или (12), записанная для бесконечной области позволяет получать фундаментальные решения.
3. Фундаментальные решения Кельвина
Фундаментальное решение системы уравнений (7), определяющее поле перемещений в неограниченной изотропной упругой среде от действия единичных сил ex и ey, строится на основе решения Кельвина (Ляв, 1935). Решение Кельвина в условиях плоской деформации можно записать в виде
здесь a=1/8πG(1-ν), rpk=[(x-ξ)2+(y-η)2] – расстояние между точками k(x,y) и p(ξ,η), β1, β2 – углы наклона радиус-вектора rpk к осям x и y соответственно в точке p(ξ,η). Компоненты перемещений (13) удовлетворяют системе дифференциальных уравнений
где u*x=u*xx+u*xy, u*y=u*yx+u*yy, G1=2G(1-ν)/(1-2ν), G2=G/(1-2ν), G – модуль упругости при сдвиге.
4. Граничные интегральные уравнения внутренних задач
Граничные интегральные уравнения двумерных задач теории упругости можно получить исходя из тождества Сомильяна , полученные на основе теоремы о взаимности работ. Погружая конечную область Ω+Г, с заданными на поверхности Г компонентами напряжений и перемещений, в неограниченное пространство, которое последовательно загружается единичными силами и описывается дифференциальными уравнениями (14), согласно теореме Бетти, получаем
здесь u*xx,...,p*yx фундаментальные перемещения и напряжения Кельвина. С учетом свойств дельта-функция Дирака
второй интеграл в правой части будет равняться ux (p), где точка p(ξ,η)∈Ω, тогда уравнение (1.21) можно представить в виде
где px,py – поверхностные напряжения, u*xx, p*xx перемещения и напряжения, возникающие в точке k(x,y) в направлении оси x от действия единичной сосредоточенной силы, действующей по этой же оси, u*yx, p*yx перемещения и напряжения, возникающие в точке k(x,y) в направлении оси y от действия единичной сосредоточенной силы, действующей по оси x. Индекс k в (17) подчеркивает, что переменным интегрирования по контуру являются координаты x,y. Формула (17) определяет перемещения по направления оси x в точке p(ξ,η) внутри области Ω при заданных значениях px,py, ux, и uy на контуре, а также объемных сил γx и γy в области Ω. Проведя аналогичную процедуру от действия единичной сосредоточенной силы, действующей по оси y, получаем
Граничные интегральные уравнения можно получить из (17) и (18) при предельном переходе, когда точка p(ξ,η) устремится к границе Г, а при этом точка k(x,y) находится на границе.
Таким образом, при переходе точки p(ξ,η) к границе области второй интеграл в (17) и (18) понимается в смысле главного значения по Коши, а остальные интегралы в обычном смысле. Следовательно, при p(ξ,η) ∈ Γ уравнения (17) и (18) преобразуются в граничные интегральные уравнения
Граничные интегральные уравнения (19) и (20) можно представить в матричной форме
где векторы перемещений, поверхностных напряжений и объемных сил представляются в виде
Симметричные матрицы коэффициентов, фундаментальных перемещений и напряжений записываются так:
U ̄* – матрица фундаментальных решений, компоненты которых соответствуют точкам внутри области Ω, в отличие от матрицы U*, где компоненты перемещений принадлежат границе Г.
Пример 4.7. Консольная балка-стенка с отверстием под действием горизонтальной нагрузки, равномерно распределенной по вертикальной грани (рис. 2). Применительно к этой задаче система алгебраических уравнений, полученная из системы граничных интегральных уравнений путем сплайновой аппроксимации нулевого порядка, представляется в виде
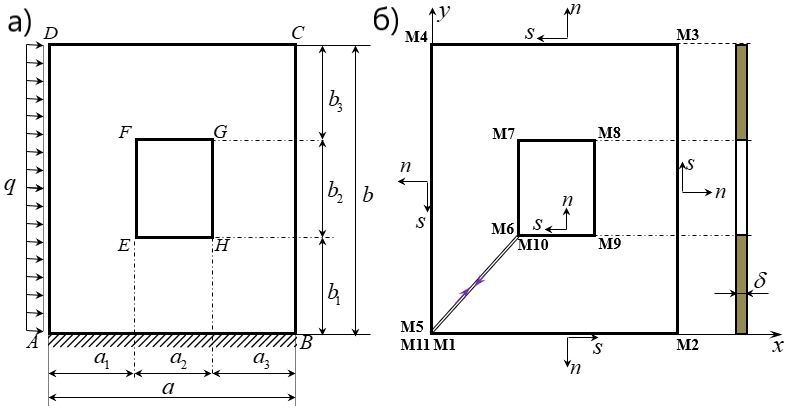
Рисунок 2 - Консольная балка-стенка
Примечание: а) - геометрия, б) - схема обхода контура
В табл. 1 результаты напряженного состояния на опорной линии AB пластинки с отверстием сравниваются c аналогичными данными для пластинки без отверстия. В угловых точках A и B напряжения определены по квадратичной аппроксимации после предварительной интерполяции результатов, полученных для узлов сплайна. Сравнение показывает, что в пластинке с отверстием примерно в 1,5 раза увеличивается нормальное напряжение в угловой точке A и касательное напряжение в середине края.
Таблица 1 - Сравнение распределения напряжений на грани
xi/h | Без отверстия | С отверстием | ||||
σy | τxy | σx | σx | τxy | σx | |
0 | -5,1940 | -2,5350 | -1 | -7,6830 | -2,5760 | -1 |
1 | -2,1900 | -1,4700 | -0,4493 | -2,4380 | -1,2650 | -1,0890 |
2 | -0,7543 | -1,0430 | 0,1886 | 0,2487 | -1,0060 | 0,0908 |
3 | -0,2769 | -0,9728 | 0,0692 | 0,7649 | -1,2800 | -0,2151 |
4 | 0,1092 | -0,8989 | -0,0273 | 0,3278 | -1,3190 | -0,1673 |
5 | 0,4850 | -0,8289 | -0,1213 | -0,1588 | -1,0550 | 0,0034 |
6 | 0,9331 | -0,7493 | -0,2333 | 0,1161 | -0,6104 | 0,0760 |
7 | 1,9990 | -0,7963 | 0,0307 | 1,8420 | -0,4456 | -0,1340 |
8 | 4,0550 | -1,0810 | 0 | 5,1160 | -0,8455 | 0 |
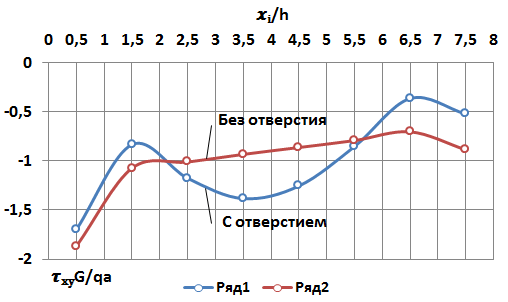
Рисунок 3 - Изменение касательного напряжения по длине защемленного края квадратной балки-стенки
5. Заключение
На основе полученных результатов можно сделать вывод, что разработанные алгоритм численного моделирования на основе метода граничных уравнений и компьютерная программа позволяют исследовать напряженно-деформированное состояние многосвязной области и могут быть использованы для расчета диафрагм жесткости многоэтажных зданий.
