On the theoretical determination of the diameter of soil stabilisation using jet grouting
On the theoretical determination of the diameter of soil stabilisation using jet grouting
Abstract
To determine the bearing capacity of a soil-cement element (SCE) in terms of both soil and material, it is necessary to know the diameter of the reinforcement. This parameter requires reliable determination, as it is a variable quantity. There are general formal approaches that do not take into account the mechanism of interaction between the solution jet and a specific soil mass. For geotechnical practice, it is important to use the strength or deformation characteristics of the soil, which would allow predicting the size of soil stabilisation zones using the most widely used single-component technology. After leaving the nozzle, the jet expands intensively and is affected by the surrounding environment. When the jet hits the wall of the well, it changes its shape and direction of movement. When the jet leaves the monitor nozzle, turbulent pulsations on its surface form irregularities in the form of waves, and as it moves away from the nozzle, the jet begins to break up into small droplets. The axial pressure and impact force of the jet decrease as it moves away from the nozzle. An ‘infinite’ increase in the radius of the borehole erosion is impossible, despite numerous repeated passes over the ‘same place’, not only because of the fading effect of the jet with distance, but also because of the likelihood of collapse of the soil arch located above.
The article presents solutions for determining the size of soil consolidation using soil deformation characteristics — elastic modulus and Poisson's ratio. Using the assessment of effective jet pressure in the well, a method is suggested for determining the size of soil consolidation zones using soil strength characteristics: cohesion C and angle of internal friction.
1. Введение
Из-за сложности происходящих процессов в грунтах при струйном закреплении многочисленные результаты, приводимые в публикациях противоречивы. Струя цементного раствора, вылетающая из сопел монитора, при своем движении увлекает за собой часть окружающей в скважине жидкости, ударяется о стенки скважины, отражается от них, смывая с поверхности частицы разрушенного грунта, создавая вихреобразные и вращательные движения в пространстве между монитором и стенками скважины, которое еще усложняется вращением буровых труб.
Струя раствора («затопленная струя» — окруженная жидкостью), попадая в объем жидкости, постепенно начинает расширяться, а ее скорость из-за сил трения с окружающей жидкостью падает. На границе струи образуются вихри, формируется пограничный турбулентный слой. На некотором расстоянии, на выходе из сопла в центральной части струи существует ядро с постоянными скоростями. С увеличением диаметра струи величина ядра быстро уменьшается. Сечение, где исчезает ядро, называется переходным и оно разделяет начальный и основной участки струи. Струя жидкости, вытекающая из сопла и встречающая стенку скважины, воздействует на нее с силой давления струи. Силу давления струи можно рассчитать с помощью уравнения изменения импульса жидкости. Таким образом, в буровой скважине гидромониторная струя, вытекающая из сопла, является турбулентной, затопленной и стесненной. Расчет такой струи производится на основе теории свободных затопленных струй .
Известно, что расчеты по определению глубины размыва грунтов струей сводятся к определению процессов воздействия гидравлических струй на грунт, и, как правило, включают три способа описания процессов: теоретические, эмпирические и «полуэмпирические». Имеется несколько подходов к описанию механизмов разрушения материала струей жидкости. Известно также, что гидродинамическое давление струи представляется как сосредоточенная сила или давление, распределенное по поверхности по некоторому закону. Давление струи вызывает в однородном грунте поля напряженно-деформированного состояния. Размеры разрушения при таком подходе определяются некоторой областью, в которой напряжения достигли предельного значения в соответствии с выбранным критерием разрушения. В качестве критериев разрушения используются такие параметры, как критическая энергия разрушения, предельная деформация, критическая скорость размыва и т.п. В подавляющем большинстве случаев используются эмпирические методы определения размеров размыва и закрепления грунтов, основанные на некотором количестве экспериментов в различных грунтовых условиях.
Рядом авторов отмечены пульсации на оси струи продольной компоненты скорости (в зоне потенциального ядра) и пульсации осесимметричной моды давления в ближнем поле вне слоя смешения . Допускается, что пульсации в области средних частот (St ∼ 0,2–0,8) являются проявлением пакетов волн неустойчивости, развивающихся в струе за счет неустойчивости Кельвина–Гельмгольца. При взаимодействии струи жидкости с твердой поверхностью могут развиваться очень высокие давления, т.е проявляется эффект гидравлического удара . Давление гидравлического удара:
где ρ — плотность жидкости, кг/м3; с — скорость волны сжатия в жидкости (≈1500м/с); v — скорость течения жидкости, м/с.
Высокоскоростные струи раствора характеризуются числом Рейнольдса и носят турбулентный характер. Турбулентность струи на ее внешней границе вызывает потери энергии с уменьшением осевой скорости из-за массообмена с грунтовой жидкостью, вихрями и вязкими касательными напряжениями. С увеличением содержания твердой фазы повышаются плотность и вязкость раствора. В результате реализуется многофакторная задача. Многочисленные результаты, приведенные в публикациях, противоречивы. Переменные параметры как гидравлические, так и грунта разнообразны, имеют большой разброс значений в зависимости от условий реализации и могут быть применимы в строго определенных условиях. Есть решения, где с увеличением давления Р и модуля упругости грунта Е, радиуса «капли» глубина разрушения грунта увеличивается
.При расчетах разрушения породы струей, как правило, выполняется единичное решение «давление-деформация» и фактический радиус закрепления грунта может не совпасть с экспериментальными значениями. Решение такой задачи не отражает эффекта «внедрения» струи в грунт, в результате которого давление от струи постепенно передается на частицы, удаленные от стенки скважины.
Грунт состоит из отдельных частиц, при встрече с поверхностью грунта струя растекается и, захватывая частицы грунта, размывает и выносит их. По мере увеличения глубины внедрения возрастает и длина пути выноса частиц, возрастает также сопротивление выносу частиц. Изменение размеров происходит за счет разрушения грунта в точке лобового действия струи и за счет размыва стенок обратными потоками. При таком подходе критерием разрушения является критическая скорость размыва либо скорость взвешивания, зависящие от гранулометрического состава грунта.
Эффективность процесса гидравлического разрушения грунтов определяется компактностью струй. К факторам, определяющим эффективность размыва грунтов струей, относятся: расход раствора; скорость истечения струй, сила удара струи, динамическое давление струи, гидравлическая мощность; геометрия монитора — число и форма сопел, углы их расположения и расстояние до стенки скважины; характеристики раствора — плотность, вязкость и т.п.; свойства грунтов — прочность, проницаемость, давление поровой жидкости.
Существенное влияние на качество закрепления оказывают величина превышения гидростатического давления над поровым и эффективная вязкость раствора.
Для закрепления грунта по струйной технологии ряд авторов
считают основополагающими механизмами взаимодействия струи с грунтами: просачивание-фильтрация в гравийных грунтах, эрозия в песках и резание в глинах. Её эффективность зависит от свойств грунтов в т.ч. от грансостава. Грунтоцемент, получаемый в песках, как правило, более однороден.Теория эрозионного разрушения разработана недостаточно. При эрозионном разрушении основными являются два вида воздействия: многократная деформация грунтов при соударении частиц раствора с грунтом и режущий износ от воздействия частиц цемента, перемещающихся по направлениям, касательным к поверхности скважины. Для пластичных грунтов основным считается режущий фактор. Одним из возможных объяснений эрозионного воздействия мониторной струи жидкости на забой скважины является кавитационная эрозия
, .Гидромониторное разрушение грунта в стволе скважины Б.И. Есьман, Г.Г. Габузов (1991) определяют:
А В.Б. Байдюк и Р.В. Винярский (1978) сделали вывод о резком снижении эффективности разрушения грунтовой породы струей с ростом дифференциального давления Pдиф. Увеличение проницаемости грунтов приводит к размыву грунтов при меньших давлениях за счет возникновения растягивающих напряжений в порах, сосредоточенных за пределами области прямого действия струи . Считается, что в песчаном грунте давление струи передается на поровую воду. Разрушение грунта происходит за счет гидроразрывов при развитии давления в поровой воде, разрывающего грунт «изнутри». Очевидно, что в этом случае в качестве критерия разрушения среды принимается ее прочность на гидростатическое растяжение. В случае песчаных грунтов со сцеплением с=0 кПа грунт не воспринимает растягивающих напряжений sp=0 кПа и размер зоны закрепления мог бы определяться только длиной действия струи и возникающими в грунте растягивающими напряжениями, но действие струи в условии пульпы в скважине быстро затухает.
Исследуя процесс разрушения грунтов под действием затопленных струй глинистых растворов с небольшим содержанием бентонитовой глины, А.К. Козодой и А.А. Босенко доказали, что разрушение консолидированных пород высоконапорной «неподвижной» струей воды без механических примесей под воздействием только гидродинамического давления практически невозможно. «Неподвижная» струя воды может вызывать кавитационное разрушение малой интенсивности.
В процессе размыва стенок скважины при струйном закреплении выделяется два основных этапа: сначала образование «воронки» путем взвешивания частиц грунта и далее при вращении монитора — врубовой полости, а при подъеме — разрушение подрезанного объема грунта. Максимальное давление на дне воронки по оси струи равно , где um – расчетная осевая скорость струи на уровне дна воронки. Диаметр получаемого ГЦЭ равен:
где dl — диаметр скважины, м; Dзакр — диаметр закрепления (размыва), м.
Теоретически сила воздействия гидромониторной «режущей» струи о вертикальную преграду рассчитывается по формуле (4):
где N — сила удара струи в непосредственной близости у насадки, Н;
m — секундный расход воды, кг/с;
ρ — плотность раствора, кг/м3;
F — площадь поперечного сечения струи, м2;
v0 — скорость вылета струи из сопла, м/с.
kф =2 (в скважине при отражении с полным разворотом струи);
Fl — полная площадь поперечного сечения струи на расстоянии l от сопла, м2:
где Pо, Pср — осевое давление струи у сопла и среднее давление струи на расстоянии l от сопла, МПа;
µ — коэффициент расхода (µ = 0,92–0,96);
K0 — коэффициент, учитывающий изменение диаметра струи высокого давления при насыщении воздухом
Ρср — средняя плотность струи у забоя, кг/м3;
vср — средняя скорость струи на расстоянии l от сопла, м/с.
Скорость вылета струи из сопла, м/с:
Н — напор воды перед насадкой, м.
где vm — осевая скорость струи в пределах основного участка; vо — начальная скорость струи при вылете из насадки; l — расстояние от сопла; rо — радиус начального участка струи; a — опытная константа ≈ 0,07.
По Г.Н. Абрамовичу (1972):
На основном участке затопленной струи полуугол её раскрытия по В.А.Жученко (1990) составляет . Используя выражение падения потока средней скорости по длине струи на расстоянии l, диаметр струи равен:
Скорость затопленной струи непрерывно уменьшается от максимального значения vm на оси струи до нуля на границе струи и среды, динамическое давление при l≥l0 также падает .
где ;
;
.
Таблица 1 - Формулы прогнозирования диаметра ГЦЭ по струйной технологии
Примечание: по источнику [11]
Имеются подходы для определения области закрепления, но для этого нужно определение специальных параметров: ударной вязкости грунтов — η (Дж/м2) или размываемости грунта — Is. Так, для определения радиуса закрепления по однокомпонентной технологии Ru кроме принятых значений dg — диаметра сопла, давления раствора — Pg, n — частоты вращения, vy — скорости подъема, ρg — плотности раствора, w/c — водоцеметного отношения, еще нужны характеристики размываемости грунта Is .
Для геотехнической практики требуется проводить расчеты с использованием физико-механических свойств грунтов (φ, с, ρ, Е, v) и параметров мониторной струи (d0, l, P) с использованием формул (4) и (11) определяя значения диаметра закрепления. Для анализа допустимо рассмотреть два теоретических подхода установления диаметра закрепления грунтов, при «однокомпонентной» струйной технологи.
2. Определение размера закрепления грунта с использованием деформационных характеристик грунтов – модуля упругости Е и коэффициента Пуассона v
Наряду с известными решениями задач Ж. Буссинеска (1885), Е. Мелана (1932) о сосредоточенной силе, приложенной к горизонтальной поверхности имеется аналитическое решение о горизонтальной силе, приложенной на глубине C внутри полупространства (Р. Миндлин, 1936) при этом поверхность z=0 свободна от нагрузок.
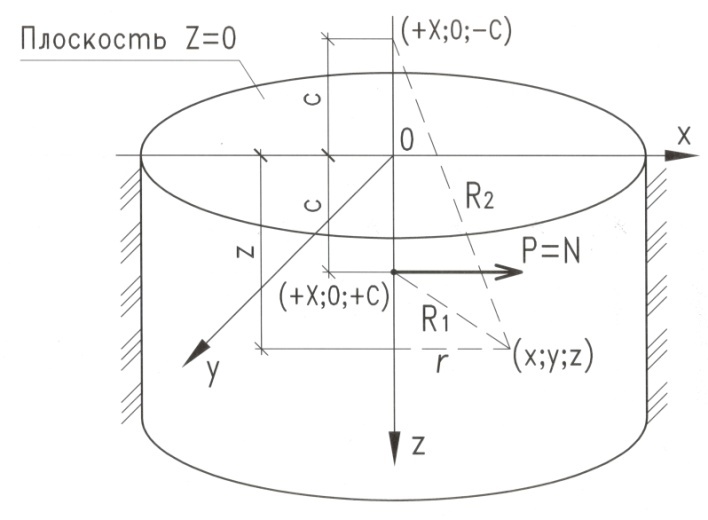
Рисунок 1 - Схема к решению Р. Миндлина для горизонтальной силы приложенной внутри упругого полупространства
С учетом (4) перемещение равно:
Напряжения σx от приложенной сосредоточенной силы на глубине z полупространства могут быть определены по формуле:
Полученные напряжения после подстановки значения силы действия струи N из формулы (4) для случая изотропных грунтов соотносятся с критерием Кулона-Мора. Критерий в главных напряжениях:
где σ1, σ2 — главные напряжения; с — сцепление; — угол внутреннего трения.
В таблице 2 приведены значения коэффициентов К1 и К2 на различных расстояниях в зависимости от коэффициента Пуассона.
Таблица 2 - Значения коэффициентов К1 и К2 для определения перемещений и напряжений от действия сосредоточенной силы внутри полупространства
№ п/п | X, м | Песок, супесь ν=0,3 | Суглинок ν=0,35 | Глина ν=0,42 | ||||||||||
К1 | К2 | К1 | К2 | К1 | К2 | |||||||||
Z= 5м | Z=15м | Z= 5м | Z= 15м | Z= 5м | Z= 15м | Z =5м | Z= 15м | Z =5м | Z= 15м | Z= 5м | Z= 15м | |||
1 | 0,15 | 1,395 | 1,385 | -57,26 | -57,26 | 1,45 | 1,44 | -59,853 | -59,853 | 1,524 | 1,512 | -64,23 | -64,23 | |
2 | 0,2 | 1,05 | 1,04 | -24,16 | -24,16 | 1,09 | 1,08 | -25,25 | -25,251 | 1,15 | 1,135 | -27,1 | -27,097 | |
3 | 0,3 | 0,70 | 0,695 | -7,158 | -7,158 | 0,732 | 0,721 | -7,482 | -7,482 | 0,77 | 0,759 | -8,03 | -8,029 | |
4 | 0,5 | 0,43 | 0,419 | -1,546 | -1,546 | 0,445 | 0,435 | -1,616 | -1,616 | 0,469 | 0,457 | -1,73 | -1,734 | |
5 | 0,6 | 0,36 | 0,350 | -0,895 | -0,895 | 0,374 | 0,363 | -0,935 | -0,935 | 0,393 | 0,382 | -1,00 | -1,00 | |
6 | 0,7 | 0,31 | 0,30 | -0,563 | -0,563 | 0,323 | 0,312 | -0,589 | -0,589 | 0,339 | 0,328 | -0,63 | -0,632 | |
7 | 0,8 | 0,274 | 0,264 | -0,377 | -0,377 | 0,28 | 0,274 | -0,395 | -0,395 | 0,299 | 0,288 | -0,42 | -0,423 | |
8 | 0,9 | 0,245 | 0,235 | -0.265 | -0,265 | 0,254 | 0,244 | -0,277 | -0,2771 | 0,2677 | 0,257 | -0,297 | -0,297 | |
Очевидно, что перемещения в первую очередь зависят от соотношения силы и модуля упругости грунта. Коэффициент К1 зависит от вида грунта, расстояния от точки приложения силы и в меньшей степени от глубины приложения силы. Напряжения σx(x,0)z=c в полупространстве зависят от величины действующей силы и коэффициента К2, а он зависит от вида грунта и расстояния от точки приложения силы и не зависит от глубины ее приложения, что не логично.
Касательные напряжения равны:
После подстановки
Для песков, суглинков и глин соотношение величин касательных напряжений на глубинах 5м и 15м близки
Полученные величины касательных напряжений, легко сравниваются с одним из критериев разрушения грунта.
3. Оценка эффективного давления струи в скважине
Для расчета закрепления грунтов оценка эффективного давления струи в скважине имеет важное практическое значение. Дифференциальное давление снижает действующее давление струи раствора на стенки скважины во время излива и представляет собой разность гидростатического и гидродинамического давлений раствора с пластовым давлением. Дифференциальное давление (формализовал П.Ф. Осипов, 2000) является комплексным фактором, с помощью которого учитываются конкретные условия скважины и свойства раствора (плотность, реологические свойства и др.) . Исследования показали, что струя способна вызвать эффект возникновения и существования обратной фильтрации (характеризуется величиной максимума скорости фильтрации). А также этот эффект способен влиять на величину и знак градиента давления. Величина Рэф — эффективное давление струи , вычисляется по формуле:
где Рос — осевое давление струи на забой, определяемое по (10); Рдиф — дифференциальное давление, определяемое по формуле:
где Ркп — потери давления в затрубном пространстве, кПа; Рпор — поровое давление, кПа; ρ — плотность раствора, кг/м3; lскв — глубина скважины, м.
Поровое давление:
где ρв — плотность грунтовых вод, кг/м3; где g — ускорение свободного падения, м/с2; L — глубина проведения закрепления от УГВ, м.
4. Определение размера зон закрепления грунта с использованием прочностных характеристик грунтов: сцепления С и угла внутреннего трения ϕ
Величина предельного давления струи малого диаметра с высоким давлением на стенку скважины рассчитывается по известной формуле Л. Прандтля и Г. Рейснера для невесомого грунта с поверхностной «пригрузкой». Это решение используется для определения осадки свай [15], для обоснования величин эксплуатационных потерь при разработке месторождений песчано-гравийных смесей землесосными снарядами . При достижении давления струи Рэф=Рu в массиве образуется область предельного состояния глубиной x. С увеличением давления струи начинаются разрушения, происходит выпор грунта и образуется «воронка», а далее врубовая полость. Величина Pu предельного давления равна:
где Рu — предельная нагрузка для невесомого грунта, приложенного на поверхности, кПа; с — удельное сцепление, кПа; — угол внутреннего трения, град.
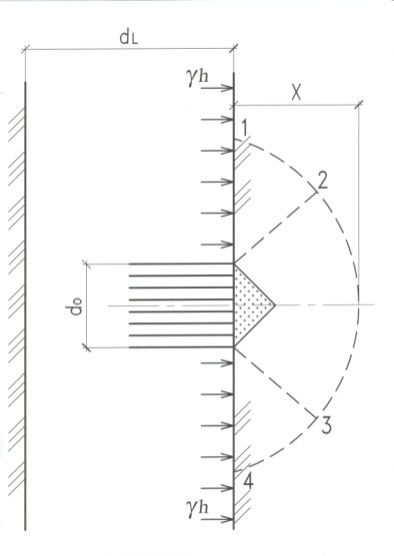
Рисунок 2 - Схема размыва струей стенки скважины в грунте
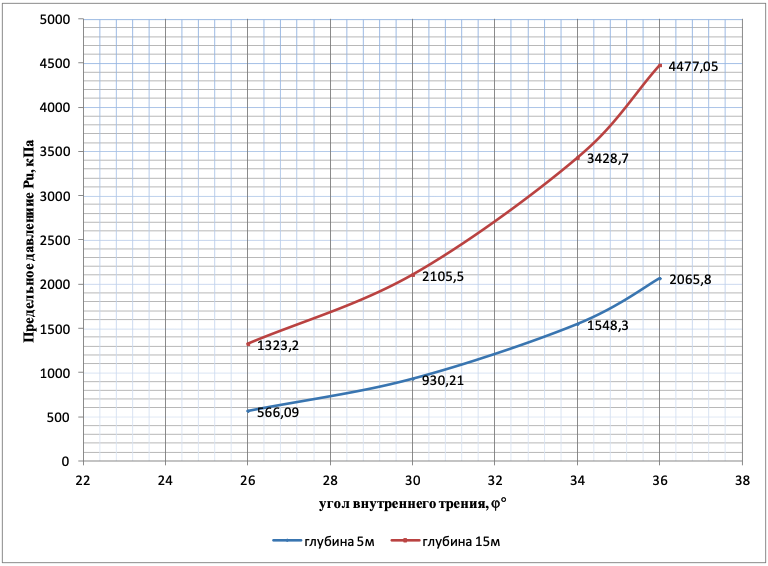
Рисунок 3 - Зависимость предельного давления Pu, кПа от угла внутреннего трения ϕ пылеватого песка (с=2-8кПа; ϕ=26-36; e=0,55-0,75) на глубинах 5м и 15м
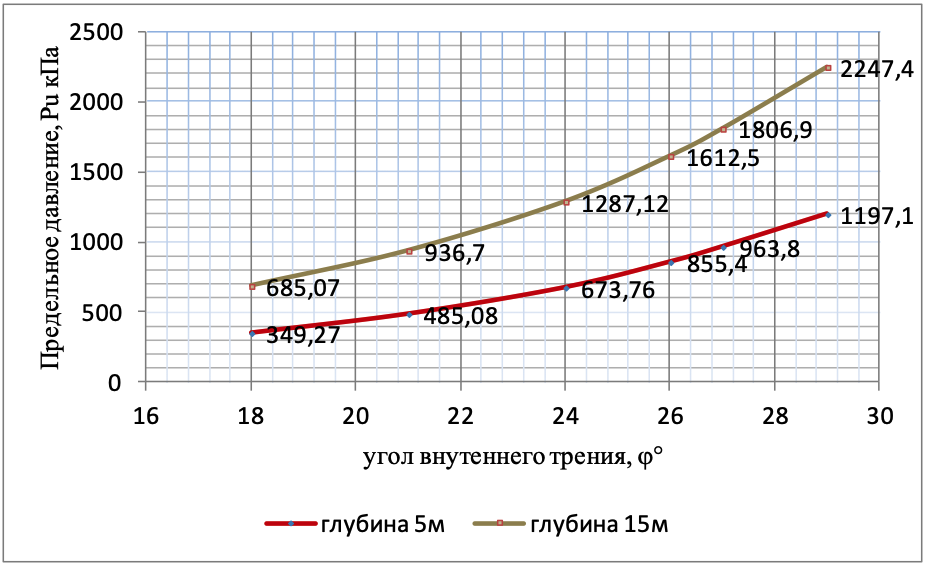
Рисунок 4 - Зависимость предельного давления Pu, кПа от угла внутреннего трения ϕ супеси (с=9-21кПа; ϕ=18-29; 0,25<Il<0,75) на глубинах 5м и 15м
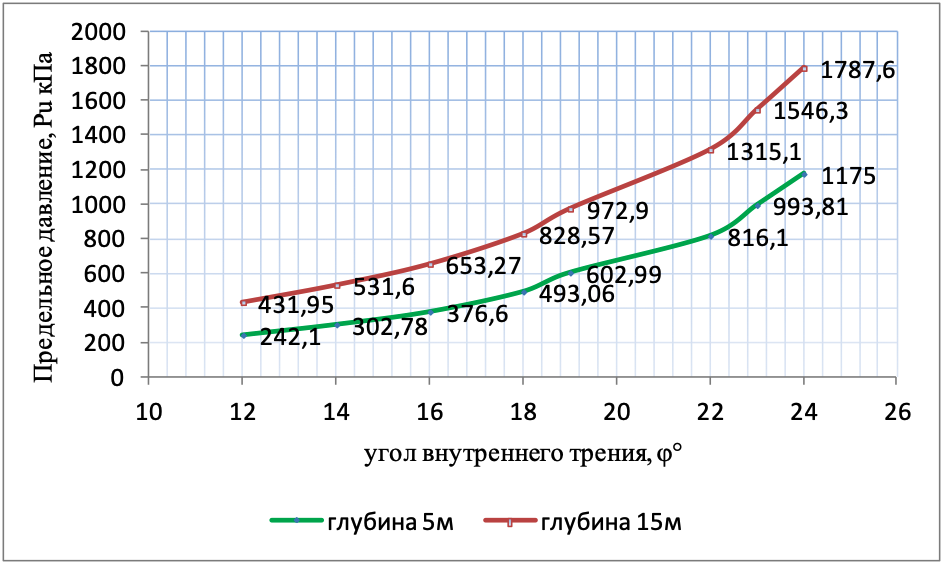
Рисунок 5 - Зависимость предельного давления Pu, кПа от угла внутреннего трения ϕ суглинка (с=12-22кПа; ϕ=12-24; e=0,55-1,05; 0,25<Il<0,75) на глубинах 5м и 15м
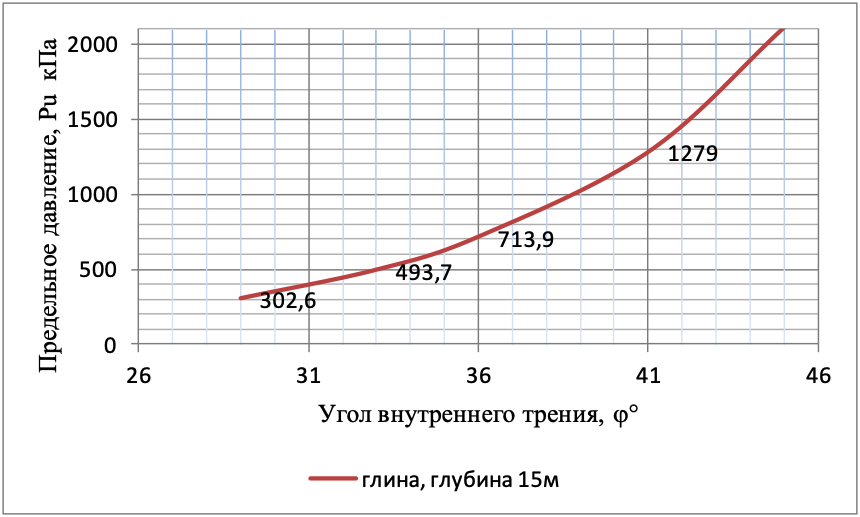
Рисунок 6 - Зависимость предельного давления Pu, кПа от угла внутреннего трения ϕ глин (с=7-15кПа; ϕ=29-45; 0,5<Il<0,75) на глубине 15м
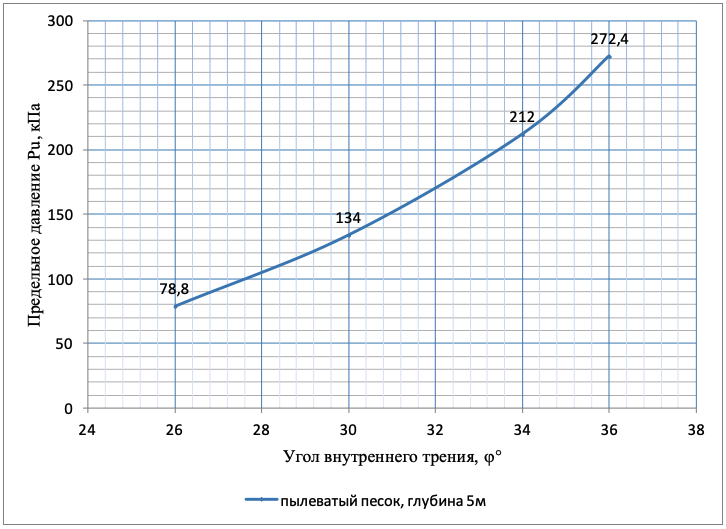
Рисунок 7 - Зависимость предельного давления Pu, кПа от угла внутреннего трения ϕ пылеватого песка (с=2 кПа; 0,7⋅ϕ=18-25°; e=0,55-0,75) на глубине 5м
Из графиков на рисунках 3 и 8 видно, что при низких давлениях нагнетания закрепление песков происходить не должно, что противоречит практическим результатам. При давлениях струи раствора 10МПа в пылеватых песках диаметр закрепления составляет ≈0,65м. Известно, что снижение сопротивления песчаных грунтов сдвигающим усилиям при воздействии вибрации весьма противоречивы (от 1,1 до 3,9 раз) и не дают четкой количественной оценки явления, объяснением которому могут быть знакопеременные изменения напряженного состояния грунта от пульсирующих нагрузок . При больших вибрационных нагрузках возможно разрушение структуры грунта с изменением формы частиц и изменением характера их взаимодействия, приводящим к уменьшению сдвиговых характеристик. Можно предположить, что ожидаемый расчетный результат достигается в результате снижения значений угла внутреннего трения на
за счет действующих пульсаций струй (рис. 7), а также снижения величины пригруза в формуле (19) и увеличения эффективного давления за счет изменения направления фильтрации поровой воды из массива внутрь скважины.
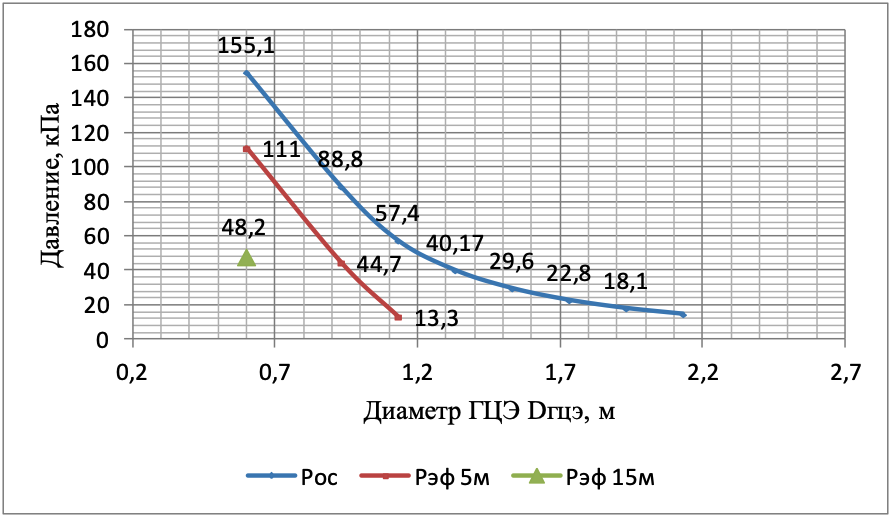
Рисунок 8 - Изменения давлений Pос и Pэф в скважинах dl=0,132м на глубинах 5м и 15м при давлении нагнетания P0=10МПа (d0=5мм)
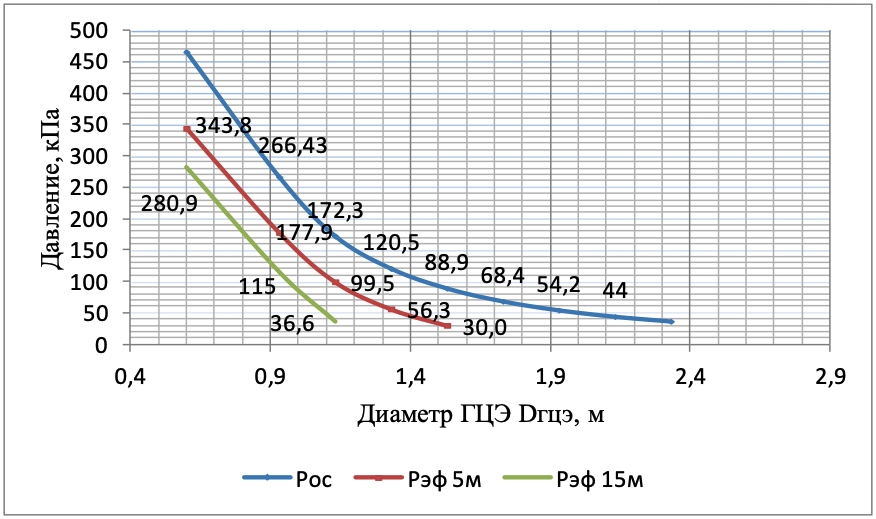
Рисунок 9 - Изменения давлений Pос и Pэф в скважинах dl=0,132м на глубинах 5м и 15м при давлении нагнетания P0=30МПа (d0=5мм)
5. Заключение
1. Для грунтов с известными модулем упругости и коэффициентом Пуассона с учетом решения Р. Миндлина для горизонтальной силы в упругом полупространстве были формализованы величины перемещений и напряжений. Перемещения от сосредоточенной силы зависят в первую очередь от соотношений силы и модуля упругости грунта. Коэффициент К1 же зависит от вида грунта, расстояния от точки приложения силы и в меньшей степени от глубины ее приложения. Напряжения в полупространстве зависят от величины действующей силы и коэффициента К2, а он в свою очередь зависит от вида грунта и расстояния от точки ее приложения и не зависит от глубины, что не является логичным.
2. Предельное сопротивление грунта определялось по формуле Л. Прандтля для слабых грунтов, залегающих на глубинах 5м и 15м. При расчетах учитывалось эффективное давление в скважине. Сопоставление расчетных значений Рu и эффективных давлений Рэф в скважинах позволяет прогнозировать диаметры закрепления цилиндрических ГЦЭ в различных грунтовых условиях и глубинах, используя стандартный набор параметров как грунтов, так и струи.
