Application of transfer functions to the calculation of equipment with non-linear vibration isolation
Application of transfer functions to the calculation of equipment with non-linear vibration isolation
Abstract
The aim of the study is to develop a method for calculating dynamic systems based on the construction of transfer and impulse response functions, allowing nonlinear differential equations of motion to be written as systems of nonlinear integral equations of the second order, which determine the complete solution of the initial system. As a result, calculated dependencies were obtained that enable the assessment of the effectiveness of nonlinear vibration isolation, in particular with additional connections, for various types of equipment with rotating parts. The effectiveness of using nonlinear vibration isolation to reduce vibrations in transient modes was calculated and demonstrated using the example of a system with three degrees of freedom.
1. Введение
Во время работы виброактивного оборудования могут возникать существенные колебания как самого оборудования, так и поддерживающих конструкций. При снижении пиковых перемещений оборудования, в частности, при проходе через резонанс, значительно снижается вероятность нарушения целостности всех систем оборудования, включая дополнительное оборудование, а также снижается передача колебаний на близстоящие конструкции, которые могут влиять на прочность и деформативность конструкций, вызывая, в частности, появление и развитие трещин. Для снижения негативного влияния колебаний применяют виброизоляцию, в том числе нелинейную.
В современных производственных процессах, где может происходить многократное включение-выключение оборудования в короткие промежутки времени, учет переходных режимов крайне важен. Однако традиционные методы анализа динамических систем, например метод «нормальных форм», не позволяют исследовать системы в переходных режимах, в которых максимальные амплитуды колебаний могут превышать уровни колебаний в эксплуатационных режимах в 3–5 раз .
2. Методология
В статье на примере оборудования с вращающимися частями, а именно вентилятора, показан алгоритм расчета виброизолированной системы с тремя степенями свободы в переходных режимах. Алгоритм расчета основан на применении передаточных функций (ПФ) и импульсных переходных функций (ИПФ) , , с помощью которого записываются, а затем строятся с помощью шагового метода по времени решения в виде сумм интегралов Дюамеля — относительно внешней и фиктивной (учитывающей нелинейные характеристики элементов систем виброзащиты) нагрузок .
Дифференциальные уравнения движения системы при нелинейной зависимости «реакция-перемещение» представляются в виде:
где sz, sx, ϑy — вертикальное и горизонтальное перемещения центра масс, угол поворота относительно оси oy (см. рис. 1), qz(t), qx(t), My(t) — равнодействующие внешних вертикальных и горизонтальных динамических воздействий, момент внешних сил относительно оси oy.
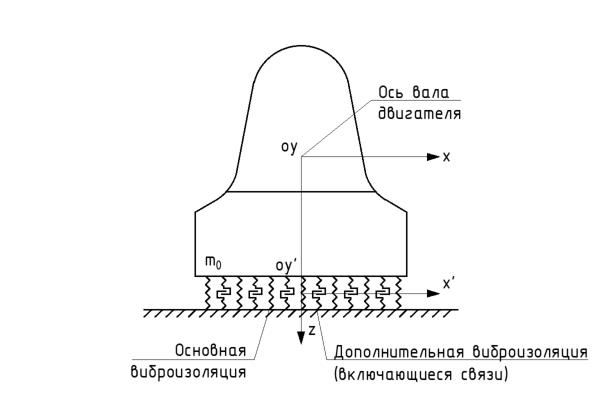
Рисунок 1 - Расчетная схема виброизолированного оборудования с включающимися связями
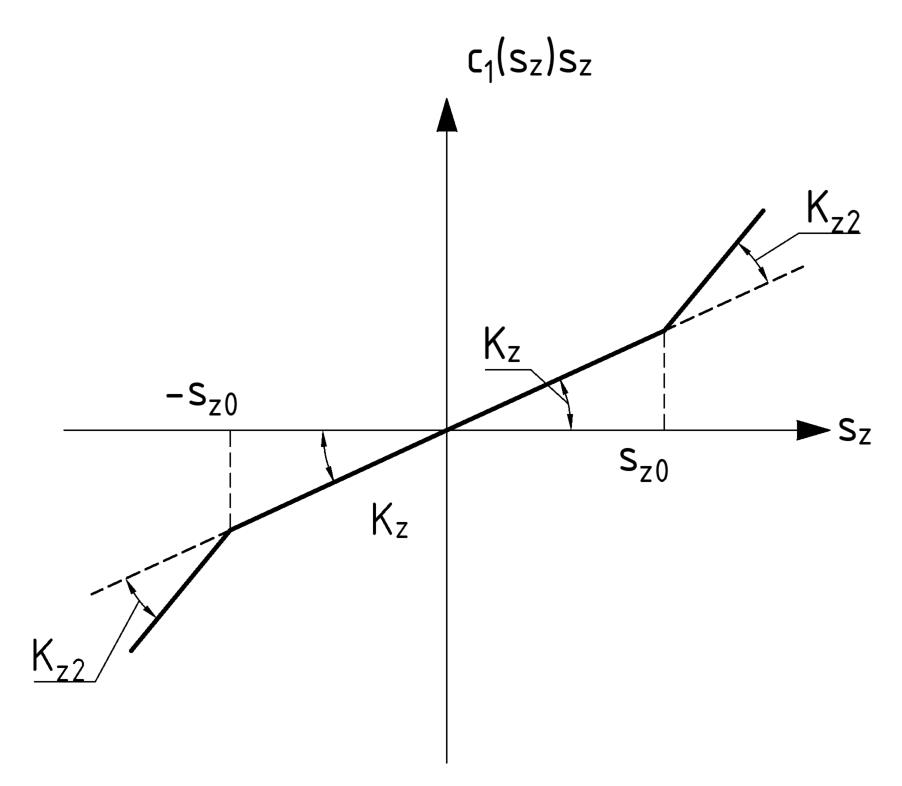
Рисунок 2 - Нелинейная зависимость реакций в упругих элементах c1(sz)sz от перемещений sz
По аналогии с (2) можно записать c2(ϑy)ϑy, c3(sz)sz, c4(sz)sz, c5(sx)sx, c6(ϑy)ϑy, c7(sx)sx.
При построении алгоритма уравнения движения системы следует преобразовать, записав нелинейные составляющие в правой части:
где для дальнейшего сокращения записей обозначено:
По аналогии с (4) можно записать Ф2(ϑy), Ф3(sz), Ф4(sz), Ф5(sx), Ф6(ϑy), Ф7(sx).
Без учета диссипативных сил выражения (4) запишутся так:
При расчете виброизолированных установок коэффициенты жесткости системы определяются, в зависимости от направления колебаний, по формулам :
где i = 1, 2,…, n — число виброизоляторов;
Kz, Kx, Kϑ — обобщённые коэффициенты жесткости основания (виброизоляторов) при вертикальном и горизонтальном смещении, при повороте относительно оси объекта соответственно;
Kzi, Kxi — жесткости i-го упругого элемента соответственно по направлениям z, x;
xi, zi — координаты центра тяжести i-го упругого элемента в системе координат z, x.
При проектировании нелинейной виброизоляции под виброактивное оборудование с вращающимися частями отмечается особенность, связанная с тем, что при вертикальном смещении оборудования жесткость основной виброизоляции Kz и жесткость дополнительных включающихся связей Kz2 суммируются (Kz + Kz2) в момент достижения оборудованием перемещений |sz| больших, чем sz0, одновременно с этим жесткости основной виброизоляции при горизонтальном смещении и повороте относительно оси суммируются с жесткостями дополнительных включающихся связей по этим же направлениям (Kzx + Kzx2; Kϑ + Kϑ2; Kxz + Kxz2; Kx + Kx2).
Таким образом, нелинейная виброизоляция влияет на уровень колебаний не только по вертикальному направлению, но и по горизонтальному направлению, при повороте вокруг оси.
Для решения системы уравнений (3) применим метод основанный на построении передаточных и импульсных переходных функций , . Передаточные и импульсные переходные функции этой системы (3), по существу, и являются решением системы нелинейных дифференциальных уравнений. Значение этих функций вычисляют из расчета линейной («порождающей») системы уравнений.
Решения нелинейной системы (3) можно записать в виде нелинейных интегральных уравнений второго рода. Общее решении системы будет определяться интегралами:
3. Основная часть
Построим передаточные и импульсные переходные функции для линейной («порождающей») системы:
Следуя общей схеме вычисления передаточных функций линейной системы , подставим в (8):
Сократим на eiωt и запишем:
Используя известные зависимости , решения подобных систем могут быть представлены в виде разложения по формам собственных колебаний при том, что каждая составляющая полного решения определяется из решения систем уравнений, диссипативные силы в которых можно учесть, добавив в каждое из них дополнительное слагаемое пропорциональное скорости колебаний.
В частности, используется модифицированная модель Фойгта с основным параметром – коэффициентом неупругого сопротивления. Такая модель принята во многих нормативных документах, где приводятся также значения этого параметра для различных материалов и сред.
Решая систему уравнений (10) методом Крамера получим:
де ΔS_z, ΔΘ_y, ΔS_x — определитель системы, в котором i столбец заменен на вектор нагрузки, Δ – определитель системы (10):
Уравнения частот собственных колебаний получим, приравняв Δ (12) нулю и положив ω=p. После преобразований представим в виде:
где
Определив значения корней частотного кубического уравнения (13) – p12, p22, p32 (значения собственных частот), знаменатель Δ (определитель) в (11) следует переписать в виде:
а функции (11) представить в виде сумм простых дробей, предварительно вычислив производную по ω2:
Следуя общей схеме вычисления передаточных функций линейной системы описанной в
, запишем ПФ системы при действии силы Q1eiωt, Q2eiωt, Q3eiωt. При учете диссипативных сил по гипотезе Фойгта в знаменатель в формулах передаточных функций следует добавить слагаемые i2vsωps2, а для модифицированной гипотезы Фойгта iγps2:где
по ист
.Hz, Hϑ и Hx — передаточные функции системы — соответственно амплитуды вертикального перемещения, угла поворота и горизонтального перемещения центра масс, записанные с учетом затухания.
Для машин с вращающимися частями, как при построении суммарных решений при гармонических воздействиях с помощью передаточных или при произвольных, используя переходные функции, перемещение от вертикальной и горизонтальной нагрузок определяются со сдвигом по фазе на π/2
:С учетом диссипативных членов могут быть записаны решения линейной системы (8) при гармонических воздействиях, в частности при qz(t)=Q1 sinωt; My(t)=Q2 l1 sinωt; qx(t)=Q3 cosωt следует:
где
Используя известные зависимости можем записать импульсные переходные функции:
где
При решении системы следует воспользоваться ИПФ для линейной системы (30)-(32). Решения нелинейной системы можно записать в виде нелинейных интегральных уравнений второго рода в виде суммы интегралов типа свертки (7). Перемещения линейной системы от действия внешних нагрузок qz(t), My(t), qx (t):
Нелинейные составляющие решения (перемещения от фиктивных нагрузок) определяются из интегральных уравнений зависящих от принятого типа нелинейности (2), (5):
где λ – прерывистая функция, равная 0 при |sz| ≤ |sz0| и 1 при |sz| > |sz0|. Знак «+» в (37), (38), (39) при sz(t) ≤ 0 и «-» при sz(t) > 0.
Для простоты вычисления интегралов ИПФ разделяют на части, зависящие исключительно от t или . Алгоритм вычисления таких интегралов показан, например, в , .
4. Результаты
Для иллюстрации применения представленного алгоритма рассмотрим задачу расчета колебаний виброизолированного массивного оборудования (вентилятора), как системы с тремя степенями свободы на произвольные динамические воздействия. Характеристика нелинейной виброизоляции представлена на рис. 1, коэффициенты жесткости системы и итоговые перемещения (углы поворота) при различных жесткостных характеристиках виброизоляции и различных значениях зазора представлены в таблице 1.
Характеристика системы:
– масса оборудования — 2400 кг;
– частота возмущающей силы ω = 157 рад/с (ƒ = 25 Гц);
– амплитудные значения внешней силы Q1= Q3=10 кН;
– эксцентриситет l1 = 0,1 м;
– момент инерции системы относительно оси oy Iy = 0,5 ⋅ 103 кг ⋅ м2;
– квадрат радиуса инерции py2 = Iy/m0 = 0,208 м2;
– величина зазора sz0.
Таблица 1 - Амплитуды перемещений в системах при различных вариантах виброизоляции
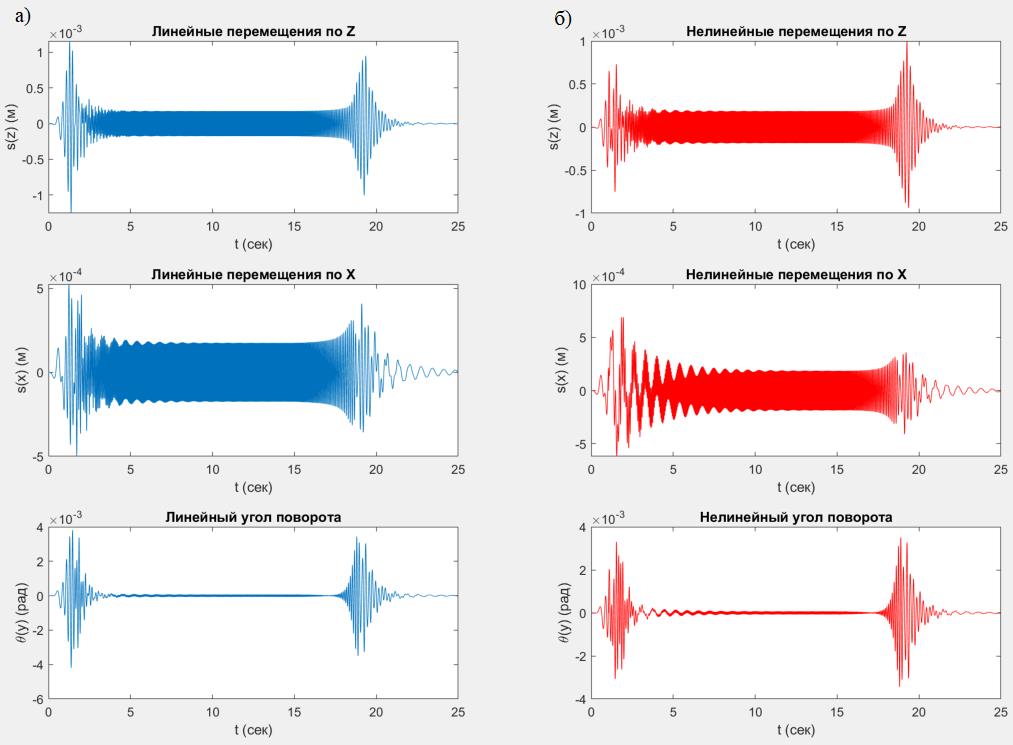
Рисунок 3 - Перемещения виброизолированного оборудования
Примечание: а – в традиционной (линейной) системе; б – в системе (нелинейной) с включающимися связями с величиной зазора sz0 = 0,5 мм
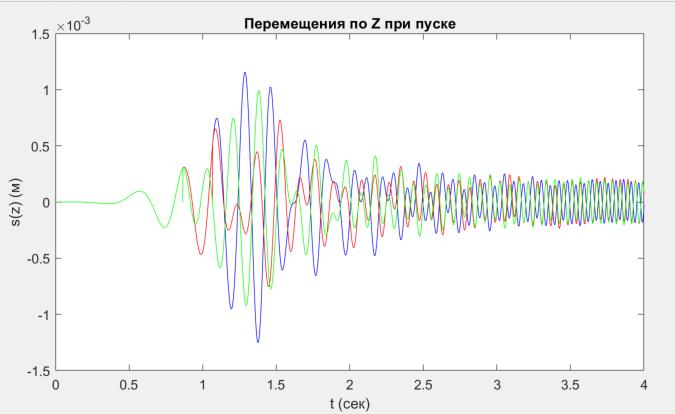
Рисунок 4 - Вертикальные перемещения виброизолированного оборудования при пуске
Примечание: синяя кривая – линейная система без зазора; зеленая кривая – нелинейная система с зазором 0,3 мм; красная кривая – нелинейная система с зазором 0,5 мм
Таким образом аналитические и численно-аналитические методы позволяют лучше понимать сущность физических процессов, например, переход через резонанс, влияние величины зазора на эффективность гашения колебаний. Также алгоритм может быть использован для расчетных обоснований проектных решений, поверочных расчетов виброизолированных установок с вращающимися частями (насосы, центрифуги, вентиляторы, турбомашины и т.д.), сравнения различных типов виброизоляции и устройства наиболее эффективной для требуемых целей.
Перспективным направлением дальнейших исследований является проведение более всестороннего и детализированного анализа различных расчетных схем, включающих разнообразные типы оборудования, нагрузки, а также различные параметры жесткости виброизоляции для подбора их оптимальных характеристик. В частности, особое внимание стоит уделить анализу виброизолированных систем с нелинейными характеристиками жесткости, изменяющимися согласно законам, таким как экспоненциальный, степенной и т.д., а также с включением в систему виброизоляции элементов с повышенным уровнем диссипативных сил — демпферов вязкого и сухого трения .
5. Заключение
1. Приведенные в статье методы и алгоритмы расчета позволяют рассматривать системы линейной и нелинейной виброизоляции в переходных режимах, а также существенно сократить этапы расчета по сравнению с методом «нормальных форм», а решения записать непосредственно относительно обобщённых, а не главных координат.
2. ИПФ представленные в виде разложения по формам собственных колебаний позволяют достаточно просто построить решения для линейных и нелинейных систем виброизоляции оборудования, в том числе со многими степенями свободы, по сути, сводящиеся к вычислению интегралов типа свёртки — от основной и «фиктивной» нагрузок.
3. При формировании расчетных программ следует учитывать особенность — учет жесткостей нелинейной виброизоляции по вертикальному, горизонтальному направлениям и при повороте вокруг оси осуществляется одновременно при достижении вертикальными колебаниями |sz| значений равными или больше sz0.
4. При оптимальном проектировании системы виброизоляции с включающимися дополнительными связями, а именно, при рациональном подборе жесткостей виброизоляторов и величины зазора, можно существенно снизить уровень колебаний системы при пуске, тем самым снизив износ оборудования и влияние на окружающую застройку, людей.
5. Применение нелинейной виброизоляции приводит к снижению уровней колебаний самого оборудования, а также к снижению реакций, передаваемых на опорные конструкции (плиты перекрытий, балки и т.д.), тем самым позволяя удовлетворить требованиям СН 2.2.4/2.1.8.566-96 «Производственная вибрация, вибрация в помещениях жилых и общественных зданий» по ограничению колебаний опорных конструкций, а также при установке оборудования на фундаменты удовлетворить требованиям СП 26.13330.2012 «Фундаменты машин с динамическими нагрузками», в котором для различных типов машин установлены наибольшие допустимые амплитуды колебаний фундаментов.
