СТАЦИОНАРНАЯ ЗАДАЧА ТЕПЛОПРОВОДНОСТИ. ПОСТАНОВКА В ПРОИЗВОДНЫХ И РЕШЕНИЕ МЕТОДОМ ГРАНИЧНЫХ ЭЛЕМЕНТОВ
СТАЦИОНАРНАЯ ЗАДАЧА ТЕПЛОПРОВОДНОСТИ. ПОСТАНОВКА В ПРОИЗВОДНЫХ И РЕШЕНИЕ МЕТОДОМ ГРАНИЧНЫХ ЭЛЕМЕНТОВ
Аннотация
В статье описана постановка стационарной задачи теплопроводности относительно производной температуры, вектора теплового потока, и ее решение методом граничных элементов. Основное преимущество постановки — возможность явного вычисления компонент вектора теплового потока без численного дифференцирования температурного поля. Граничные интегральные уравнения получены относительно вектора теплового потока. Изложена процедура решения основных и смешанных краевых задач, составлены системы разрешающих уравнений. На примере численного решения смешанной краевой задачи теплопроводности с граничными условиями третьего рода и сопоставления результатов расчета показана достоверность предлагаемой постановки и требуемая точность полученного решения.
1. Введение
Задача стационарного распределения температуры в твёрдом теле — одно из фундаментальных приложений уравнений Лапласа и Пуассона, изучаемое ещё со времён Фурье. До разработки численных методов её решали аналитически для областей простой геометрии; классические решения обобщены в нескольких монографиях , . Однако в инженерной практике преобладают тела со сложной конфигурацией и неоднородными граничными условиями, где строгое решение недостижимо.
Среди численных подходов метод граничных элементов (МГЭ) занял особое место, поскольку позволяет свести расчёт к дискретизации лишь границы области, и тем самым на единицу снизить размерность задачи. В работах , , , представлена реализация метода граничных элементов для наиболее характерных процессов, описываемых уравнением Лапласа, для задач теплопроводности. Также, применительно к уравнению Пуассона, МГЭ нашел широкое применение при решении задачи о кручении стержней , так как при любой геометрии сечения стержня экстремальные значения касательных напряжений локализуются именно на границе . Следовательно, определение касательных напряжений на границе позволяет сделать однозначный вывод о прочности всего сечения. Помимо решения внутренних краевых задач, МГЭ крайне эффективен при решении так называемых внешних краевых задач или задач на бесконечной или полубесконечной области . В классической постановке МГЭ интегральное представление формулируется относительно температуры, а тепловой поток получают последующим дифференцированием, что порождает дополнительные погрешности и приводит к ухудшению сходимости на участках с большими градиентами.
Настоящая работа предлагает альтернативную постановку — непосредственно в частных производных, где основным искомым полем является вектор плотности теплового потока. Такой подход позволяет исключить промежуточный этап численного дифференцирования и тем самым снизить накопление погрешности.
В статье выводится интегральное уравнение для вектора теплового потока, описываются алгоритмы сборки матриц МГЭ, а также приводится схема их эффективной реализации. Методика проходит верификацию на тестовой задаче с известным аналитическим решением; анализ результатов расчета подтверждает высокую точность и стабильность предложенного подхода даже при грубой дискретизации границы. Полученные результаты демонстрируют перспективность постановки относительно производных для практических расчётов теплопроводности в инженерных приложениях.
Цель работы — разработка постановки задачи стационарной теплопроводности относительно вектора теплового потока для любых типов граничных условий; получение граничных интегральных относительно теплового потока и решение методом граничных элементов.
2. Постановка задачи относительно вектора теплового потока
Рассмотрим плоскую область S, ограниченную контуром Γ (рис. 1). Традиционную формулировку задачи о стационарном распределении температуры T = T (x, y) в области S запишем следующим образом:
где d = d (x, y) — заданная функция источников тепла;
T = T1 (Г) — заданная на Г1 температура;
p = p (Г) — заданный на Г2 тепловой поток;
— производная по нормали к контуру Г;
Г = Г1 + Г2 — части граничного контура Г;
— оператор Лапласа на плоскости, здесь
Рисунок 1 - Расчетная схема
Тогда уравнение (1) запишется следующим образом:
Функция qx, qy удовлетворяют уравнению
которое естественно назвать уравнением совместности.
Выполним следующие операции: продифференцируем уравнение (5) по x и вычтем уравнение (6), продифференцированное по y; продифференцируем уравнение (5) по y и сложим с уравнением (6), продифференцированным по x.
Получим следующие два уравнения
Сформируем граничные условия, записанные относительно неизвестных функций qx и qy. Так как по определению нормальной производной
где nx и ny — проекции вектора единичной нормали на оси координат (рис. 1),
то искомый вид условия (3) следующий
Для формулировки второго граничного условия продифференцируем по дуге контура Γ условие (2)
где tx и ty, — проекции единичного касательного вектора к контуру Γ (рис. 1);
— известная на Γ функция.
Для обеспечения необходимого числа граничных условий, потребуем: в точках границы Г1 — выполнения уравнения (5), в точках границы Г2 — выполнения уравнения (6).
Окончательно для неизвестных функций qx и qy имеем следующие уравнения и граничные условия:
Система дифференциальных уравнений (11) с граничными условиями (12) и (13) и представляет предлагаемую постановку краевой задачи, неизвестными в которой являются производные от решения задачи (1)–(3). Постановку (11)–(13) будем называть постановкой (задачей) относительно производных. Решив задачу (11)–(13), можно найти производные от температуры T, не находя самой функции T. Поскольку в численных алгоритмах решения этой задачи в качестве узловых неизвестных будут выступать значения функций qx и qy, то, тем самым, исчезает проблема численного дифференцирования температуры для их определения.
Ниже представлена векторная запись постановки (11)-(13) с необходимыми пояснениями. Обозначим q –вектор с компонентами qx, qy; — оператор-градиент на плоскости; вектор
— повернутый на π/2 по часовой стрелке, если смотреть с оси z, вектор q; n и t — единичные нормальный и касательный к контуру Γ векторы; точкой обозначается скалярное произведение. Постановка задачи (11)–(13) приобретает следующий вид:
3. Интегральное представление и граничные интегральные уравнения относительно вектора теплового потока
Для получения граничных интегральных уравнений относительно вектора теплового потока необходимо иметь интегральное представление на плоскости для вектора q.
Пусть a — единичный тензор на плоскости, c — базисный кососимметричный тензор на плоскости. Если ex, ey — орты декартовой системы координат, то введенные тензоры имеют следующие диадное представление:
Основные свойства введенных тензоров:
гдe — произвольный вектор на плоскости
— повернутый на π/2 вектор
Лапласиан от произвольного вектора имеет следующий вид:
Умножим (17) скалярно на произвольный вектор q, преобразуя правую часть с помощью равенства :
где Q — произвольный тензор второго ранга
символ «∙∙» — двойное скалярное произведение двух тензоров ;
получим:
Интегрируя (19) по области S и используя формулу Остроградского-Гаусса
справедливую для любого вектора b, получим:
где ,
— проекции вектора q на нормаль и касательную к контуру Γ; n, t — единичные векторы (рис. 1), связанные соотношениями:
Пусть m, z — две произвольные точки на плоскости, Rm, Rz — их радиус-векторы (рис. 2). Введем обозначения:
Введем функцию v (x, y) — фундаментальное решение уравнения Лапласа на плоскости :
Рисунок 2 - Определение радиус-векторов
— оператор Лапласа с дифференцированием по координатам точки z;
— дельта-функция Дирака со следующим основным свойством:
здесь — произвольная непрерывная функция;
обозначение подчеркивает, что интегрирование ведется по координатам точки z;
Воспользуемся уравнениями (23)-(25) и положим в равенстве (21) , где b — произвольный постоянный вектор. Для вектора
имеем:
Подставляя в (21) и используя свойство (26), получим (отбросив произвольный вектор b):
Равенство (29) и есть искомое интегральное представление произвольного вектора на плоскости.
Если под вектором q понимать вектор производных от температуры T: q = qxex + qyey, то для него, согласно (5), (6)
уравнение (29) приобретает следующий вид
Чтобы иметь возможность вычислить q в любой точке m ∈ S необходимо в каждой точке границы Γ знать значения нормальной и касательной составляющих qn и qt. В основных краевых задачах известна только одна из этих составляющих или их линейная комбинация:
– I краевая задача,
– II краевая задача.
I краевая задача.
Для нахождения функции qn умножим (31) скалярно на вектор nm (единичный вектор, нормальный к контуру Γ в точке m) и наложим условие m ∈ Г. Получим следующее интегральное уравнение относительно функции qn:
Определив из этого уравнения неизвестную функцию qn, по (31) возможно вычислить значение вектора q в любой точке m ∈ S.
II краевая задача.
Для нахождения функции qt умножим (31) скалярно на вектор tm (единичный вектор, касательный к контуру Г в точке m) и наложим условие m ∈ Г. Получим следующее интегральное уравнение относительно функции qt
Уравнение (33) относительно неизвестной функции – граничное интегральное уравнение для II краевой задачи.
Любое из уравнений, (32) или (33) может быть использовано при решении смешанной краевой задачи, где неизвестными являются и нормальная и касательная компоненты вектора теплового потока q.
III краевая задача.
В задачах теплопроводности широкое применение также находят граничные условия 3 рода (условие Робина). Если тепловой поток через поверхность линейно пропорционален разности температур между поверхностью и окружающей ее средой, то такое граничное условие принято называть линейная теплопередача в среду с температурой T0. Условие Робина представляет собой линейную комбинацию температуры и ее производной по нормали:
где k, e, f — функции положения точки. Условие (34) включает в себя упоминаемые ранее условия, поскольку при f = 0 получаем условие Дирихле, при e = 0 имеем условие Неймана.
Для решения третьей краевой задачи воспользуемся классическим граничным интегральным уравнением относительно функции температур T :
где — фундаментальное решение уравнения Лапласа на плоскости;
Используя уравнение (34) заменим функцию температур T на функцию qn уравнении (35):
Решив полученное уравнение и найдя функцию qn на границе Г, функцию qt можно определить с помощью уравнения второй краевой задачи (33).
Интегральные уравнения (32), (33) отличаются только правой частью. Оба уравнения — уравнения второго рода, следовательно, решение второй краевой задачи аналогично по сложности решению первой краевой задачи.
Численное решение уравнений (32), (33) может быть выполнено методом граничных элементов (МГЭ), который применяется при решении обычных граничных интегральных уравнений в постановке относительно функции температур T. При этом уравнения (32), (33) и интегральное представление (31) обеспечивают возможность определения теплового потока q как на границе, так и внутри области без численного дифференцирования функции температур T.
4. Метод граничных элементов
Рассмотрим наиболее полную задачу, в которой имеются все три упомянутые выше граничные условия: Дирихле, Неймана, а также их линейная комбинация — условие Робина.
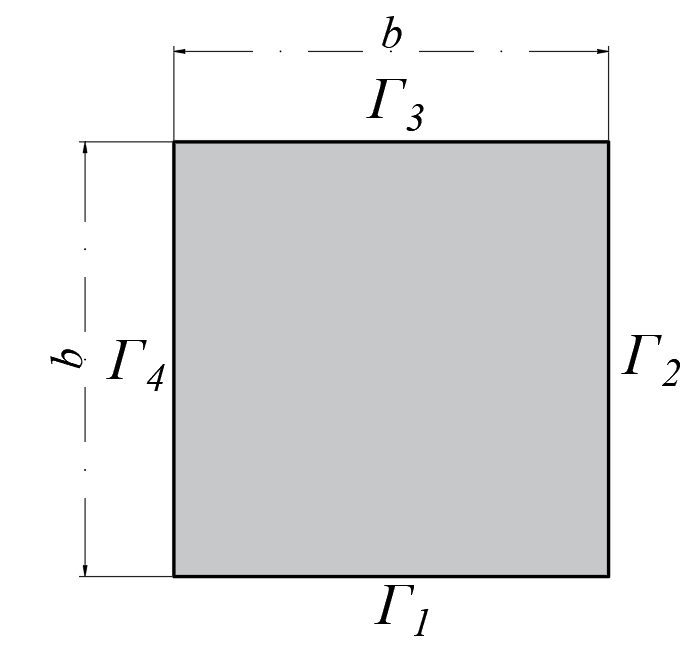
Рисунок 3 - Расчетная схема смешанной краевой задачи
Поскольку в данном примере на границе Г задано граничное условие III рода, такую задачу следует решать в два шага. На первом шаге необходимо численно решить уравнение (37) и определить функцию qn на всей границе Г. На втором — используя уравнение (33), численно определить функцию qt на границе Г.
Запишем дискретную форму интегрального уравнения (35), с использованием так называемых «постоянных» граничных элементов. Узлы, в которых рассчитываются значения неизвестной функции расположены в середине каждого элемента. Значение искомой функции в пределах одного граничного элемента принимается постоянной величиной. Для упрощения записи разобьем границу на 4 элемента (размер граничного элемента l = b) и преобразуем уравнение (35) к виду:
Введем обозначения
где — дельта Кронекера;
l — длина граничного элемента
и представим уравнение (38) в матричном виде
где
Подставив формулу (42) в уравнение (41), получим
Система уравнений относительно Q примет следующий вид
Используя уравнение (46), можно определить функцию на всей границе Γ.
Выполним аналогичные операции для граничного интегрального уравнения второй краевой задачи. Дискретная форма уравнения (33) примет следующий вид
или в матричном виде
где z — столбец узловых значений касательной компоненты вектора теплового потока qt на границе Γ;
Представленное решение описывает наиболее общую постановку решения смешанной краевой задачи, в которой также имеются граничные условия третьего рода.
5. Результаты и обсуждение
Для верификации методики выполним расчет описанной выше задачи. Рассмотрим распределение компонент вектора теплового потока по границам Г1-4. Аналитическое решение исследуемой задачи имеет следующий вид ,
где an — положительные корни уравнения an tg (an b) = 1.
Расчеты выполнены с последовательным двукратным уменьшением размера граничного элемента (1, 0.5, 0.25). Размеры граничных элементов приняты одинаковыми по всему контуру Γ. На рисунке 4 представлены результаты расчета.
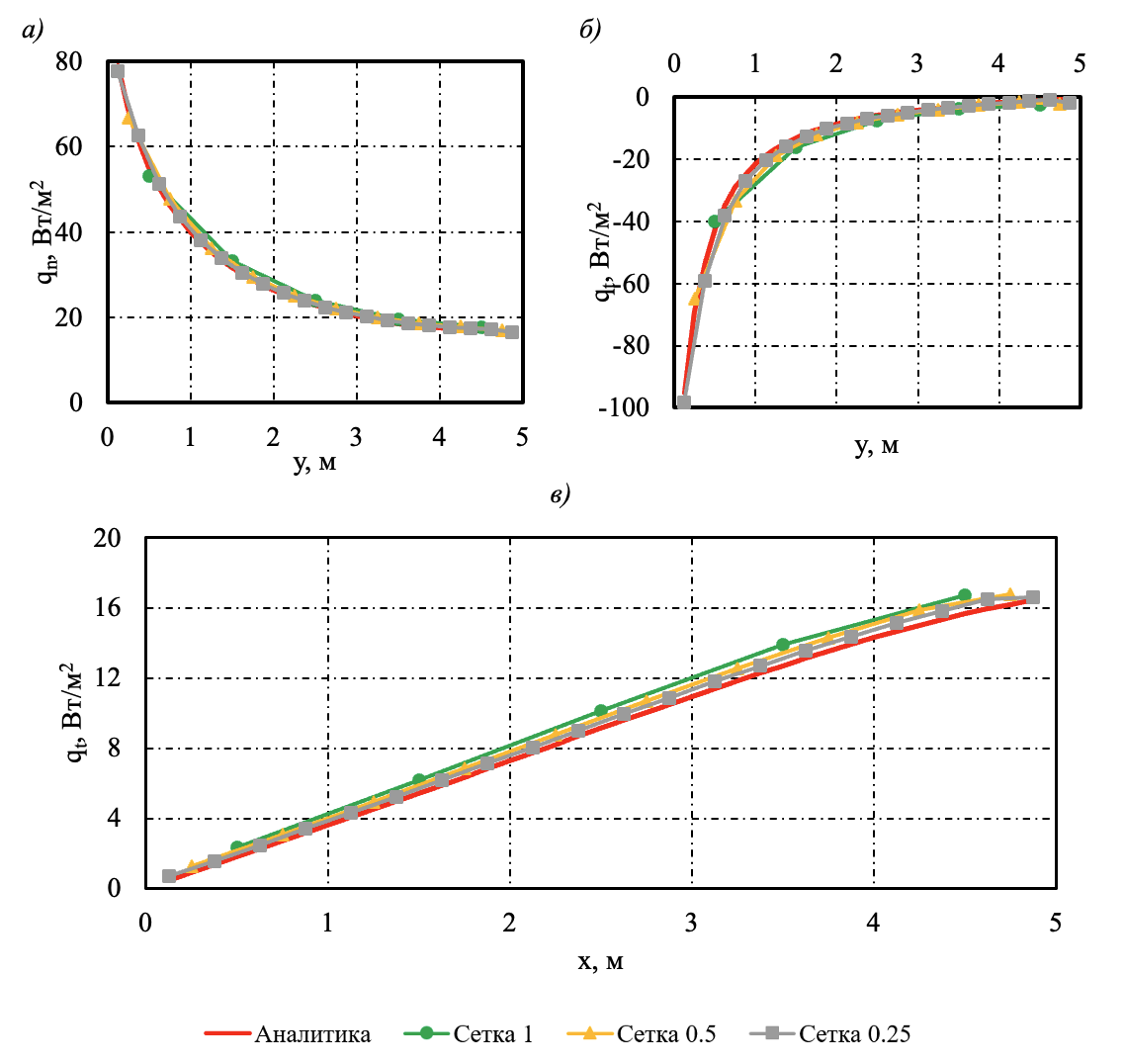
Рисунок 4 - Результаты расчета тестовой задачи
Примечание: а – qn на границе Γ2; б – qt на границе Γ2; в – qt на границе Γ3
6. Заключение
В работе представлена постановка задачи стационарной теплопроводности относительно вектора теплового потока, получены граничные интегральные уравнения для основных, в том числе смешанных краевых задач. На примере решения смешанной задачи с граничными условиями третьего рода описан алгоритм решения методом граничных элементов, проведена верификация с известным аналитическим решением. Полученные результаты демонстрируют возможность решения основных краевых задач, которые представляют собой уравнения Лапласа или Пуассона, относительно производной исходной функции.
