Численное моделирование коррозии в преднапряженном железобетонном изгибаемом элементе
Численное моделирование коррозии в преднапряженном железобетонном изгибаемом элементе
Аннотация
Коррозия арматуры является одним из ключевых факторов, снижающих долговечность и несущую способность предварительно напряженных железобетонных конструкций, особенно работающих в агрессивных средах. В статье рассмотрены вопросы разработки и верификации достоверных численных моделей для оценки остаточного ресурса коррозионно-поврежденных предварительно напряженных конструкций является актуальной задачей, позволяющей перейти от качественных оценок к прогнозированию их поведения и обоснованию ремонтных мероприятий.
В работе выполнено конечно-элементное моделирование в программном комплексе ANSYS. Для описания поведения бетона использована конститутивная модель Menetrey-Willam, для арматуры — билинейная диаграмма с упрочнением. Проведена верификация моделей на экспериментальных данных для балок с различной степенью коррозионного повреждения арматуры и соответствующими потерями предварительного напряжения. На основе верифицированной методики выполнен анализ полноразмерной подкрановой балки таврового сечения.
Установлена сходимость (85–90%) результатов численного моделирования с экспериментальными данными, что подтверждает корректность выбранных моделей материалов, типов конечных элементов и граничных условий. Показано, что коррозионные повреждения и сопутствующая потеря предварительного напряжения приводят к значительному снижению несущей способности изгибаемых элементов. Для коррозионно-поврежденных балок с высоким процентом потерь (60%) и для балок без предварительного напряжения характер разрушения меняется: предельное состояние достигается не при достижении текучести арматуры, а вследствие хрупкого разрушения бетона.
Полученные результаты позволяют проводить достоверную оценку влияния коррозии на напряженно-деформированное состояние и несущую способность реальных предварительно напряженных конструкций, что необходимо для прогнозирования их остаточного ресурса и разработки стратегий обслуживания и усиления.
1. Введение
В данной статье приведены расчеты экспериментальных образцов изгибаемых железобетонных элементов в программном комплексе Ansys. Актуальность работы обусловлена необходимостью оценки влияния коррозии арматуры на несущую способность предварительно напряженных железобетонных конструкций , особенно ответственных, таких как подкрановые балки. Коррозия приводит к уменьшению сечения арматуры и потере предварительного напряжения , что может вызвать перераспределение усилий и хрупкое разрушение. Эксплуатация предварительно напряженных железобетонных конструкций в условиях агрессивных сред, характерных для многих промышленных предприятий (химических, металлургических, целлюлозно-бумажных комбинатов), приводит к развитию коррозионных процессов в арматуре. Особую уязвимость демонстрируют ответственные изгибаемые элементы, такие как подкрановые балки, работающие под воздействием значительных динамических и статических нагрузок. Коррозия напрягаемой арматуры является комплексной проблемой, приводящей не только к уменьшению площади поперечного сечения канатов, но и к потере предварительного напряжения, ухудшению сцепления с бетоном, а также к инициированию и развитию трещин в бетоне. Совокупность этих факторов существенно снижает несущую способность, жесткость и долговечность конструкций, создавая риски аварийных ситуаций и требуя значительных затрат на ремонт и усиление.
В качестве объекта экспериментального исследования были выбраны предварительно напряженные железобетонные балки прямоугольного сечения размерами 100×150 мм и длиной 1200 мм. Образцы армировались высокопрочными семипроволочными канатами классов К1400, которые подвергались предварительному натяжению с контролем усилий тензодатчиками. Особенностью методики являлось моделирование коррозионного повреждения на участке чистого изгиба. Для этого на этапе подготовки на канаты накладывались электроды с шагом 200 мм для проведения управляемой ускоренной электрохимической коррозии в 7% растворе хлорида натрия, позволяющей достичь целевых степеней повреждения 20% и 30% сечения.
Коррозионное повреждение в численном моделировании реализовывалось через поэтапное уменьшение площади поперечного сечения канатов и соответствующее снижение уровня предварительного напряжения. Учет ослабления сцепления на поврежденных участках в модели не задавалось, так как конструкция предполагает работу арматурного каната за счет закладных упорных элементов.
Актуальность проведения детальных экспериментальных и численных исследований в данной области обусловлена недостаточной изученностью количественного влияния различных степеней коррозионного повреждения на остаточный ресурс предварительно напряженных элементов. Существующие нормативные методы расчета, как правило, не предусматривают прямого учета снижения прочностных и деформационных характеристик материалов вследствие коррозии, что может приводить к неконсервативным оценкам несущей способности и запаса надежности эксплуатируемых конструкций.
Целью настоящего исследования являлось комплексное численное и экспериментальное изучение влияния коррозии преднапрягаемых арматурных канатов на прочностные и деформационные характеристики железобетонных балок при статическом и циклическом нагружении. Для достижения поставленной цели решались следующие задачи: разработка методики проведения ускоренной электрохимической коррозии образцов с заданными уровнями повреждения; экспериментальное определение изменения механических свойств арматурных канатов после коррозии; исследование несущей способности, деформативности (прогибов) и характера разрушения балок-образцов; анализ кинетики образования и раскрытия трещин; построение и верификация конечно-элементной модели, учитывающей уменьшение сечения арматуры, потерю преднапряжения и ослабление сцепления; установление количественных зависимостей между степенью коррозии, потерей предварительного напряжения и снижением нагрузочной способности элемента.
2. Методы и принципы исследования
Работа бетона описывалась с помощью модели Menetrey-Willam. Модель Menetrey-Willam, как правило, лучше подходит для моделирования поведения связанных заполнителей, таких как бетон, чем например модель Drucker-Prager , .
В качестве основы данная модель использует теорию пластического течения. Модель бетона состоит из трех основных компонентов:
1) Трехинвариантная предельная поверхность fMW, описываемая уравнением:
где, с2 и с3 параметры уравнения, контролирующие форму меридионального сечения поверхности и определяемые на основании пределов текучести при одноосном растяжении (Rt), сжатии (Rc) и двухосном сжатии (Rb) .
2) Поверхность пластического потенциала , отвечающая за направление вектора пластических деформаций
где ψb — угол дилатации бетона при одноосном сжатии, который представляет собой результат деления нормы тензора объемных пластических деформаций на норму девиатора тензора пластических деформаций; Bg и Cg параметры, характеризующие пластический потенциал. Значения угла дилатации в зависимости от класса бетона построены на основании допущения, согласно которому при достижении поверхности прочности в области одноосного сжатия полные объемные деформации равны нулю :
3) Законы эволюции предельной поверхности, отвечающие за упрочнение и разупрочнение материала. В модели предусмотрены раздельные законы эволюции для сжатия и растяжения (см. рис. 1):
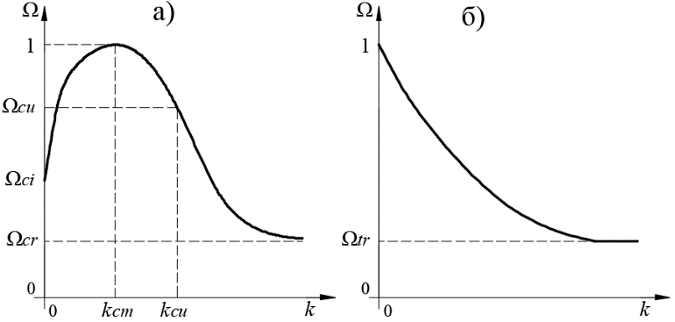
Рисунок 1 - Графическая интерпретация законов эволюции предельной поверхности при сжатии (а) и растяжении (б)
Параметры модели бетона. В расчетах использован тяжелый бетон класса В25. Нормативные и расчетные характеристики бетона приняты согласно СП 63.13330.2018:
Нормативное сопротивление осевому сжатию – Rbn = 18,5 МПа.
Нормативное сопротивление осевому растяжению – Rbtn = 1,55 МПа.
Модуль упругости бетона, Eb = 30000 МПа.
Коэффициент Пуассона, ν = 0,2.
Для задания модели Менетрея–Виллама в ANSYS использованы следующие ключевые параметры:
Предел прочности при одноосном сжатии, fc=Rbn=18,5 МПа.
Предел прочности при одноосном растяжении, ft=Rbtn=1,55 МПа.
Отношение пределов прочности при двухосном и одноосном сжатии, fbc/fc=1,16.
Отношение прочности при растяжении-сжатии к прочности при одноосном растяжении, ftb/ft=1,28.
Угол дилатансии (расширения) Ψ= 15°.
Параметром, характеризующим разупрочнение материала при растяжении, является энергия разрушения GF . Данный параметр представляет собой количество энергии, которое необходимо сообщить материалу для того, чтобы прекратить передачу напряжений между берегами трещины (полностью разорвать межатомные связи). Величина энергии разрушения может быть найдена по формуле (8) согласно исследованию . Концепция применения подобного способа регуляризации в рамках модели бетона ранее рассматривалась в работе .
Поведение стали описывалось билинейной зависимостью с упрочнением (рис. 2).
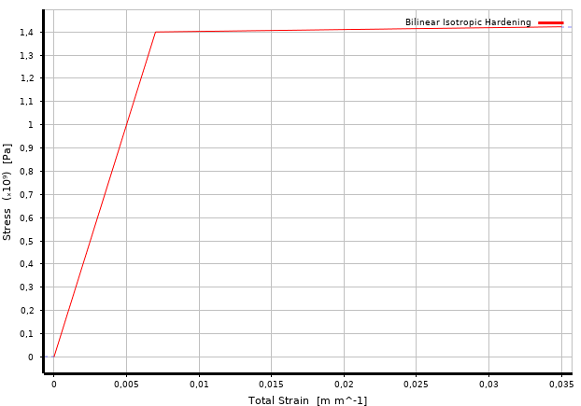
Рисунок 2 - Билинейная диаграмма деформирования арматуры
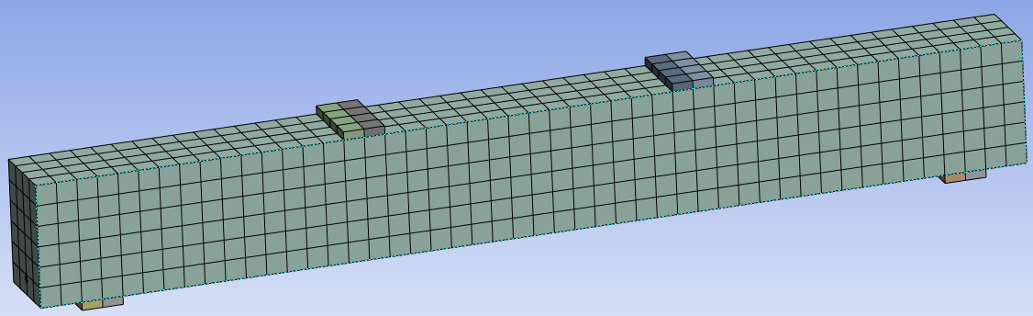
Рисунок 3 - Общий вид модели с разбиением на конечные элементы
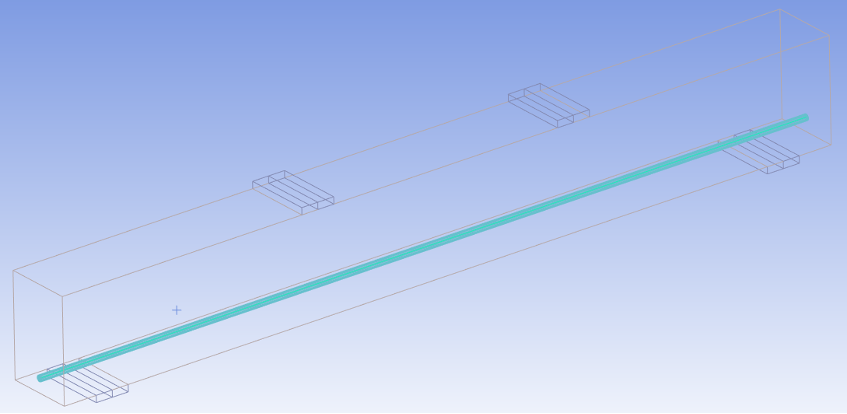
Рисунок 4 - Общий вид модели с армируемым стержнем
Расчет модели выполнялся в два этапа, на первом этапе создавалась предварительное напряжение в балке, на втором этапе прикладывалась нагрузка через две металлические пластины, моделирующая экспериментальное нагружение.
Предварительное напряжение арматуры в численной модели выполнялось с помощью изменения температуры бетона, в результате заданные линейные температурные расширения арматуры как 1,2*10-5 приводили к возникновению растягивающих усилий, тем самым создавая разные степени преднапряжения балки (рис. 5).
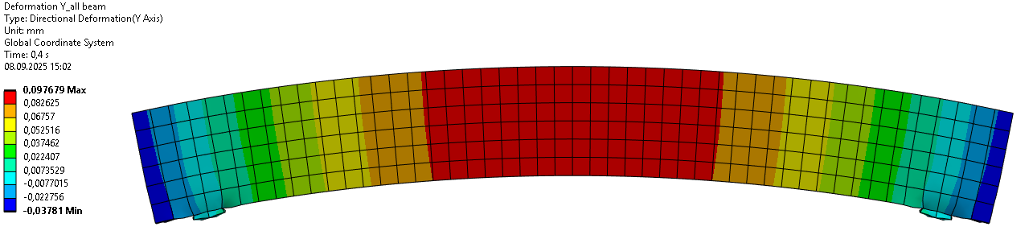
Рисунок 5 - Выгиб балки после предварительного напряжения арматуры
Для проведения экспериментальных исследований были запроектированы и изготовлены 6 железобетонных образцов — балок прямоугольного сечения размерами 100x150 мм длиной 1200 мм. Диаметр закладываемого арматурного каната для 2-х групп по три образца составлял 9,6 мм, 12,5 мм. Также на этапе подготовки накладывались провода для корродирования в агрессивной среде каждые 200 мм по длине каната, оставляя в качестве анкеровки по 300 мм с каждой стороны. Усилие передавалось через заложенные цанги в теле бетона.
Сечение экспериментальной балки приведено на рисунке 6. Схема изготовление образцов продемонстрирована на рисунке 7.
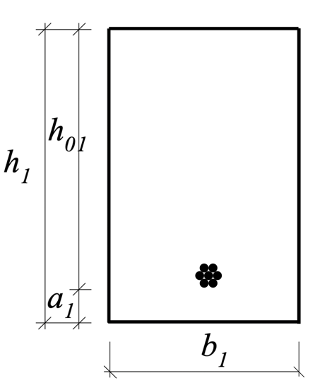
Рисунок 6 - Сечение экспериментальной железобетонной балки

Рисунок 7 - Изготовление железобетонных балок-образцов

Рисунок 8 - Корродирование железобетонных образцов
где γs — плотность стали, 7850 кг/м3;
ZFe, MFe, F — характеристики стали,
∆ds — разница между диаметром каната до и после корродирования, как целевые ставились 20 и 30%,
Получаем, что скорость коррозии для достижения 4-х образцов коррозии в 20% должна составлять
То есть, для поставленной задачи подаваемая сила тока составила 2,1 А. Подробно методика ускоренной коррозии описана и продемонстрирована в работе .
Далее были исследованы изменения прочности и деформативности изгибаемых железобетонных балок после корродирования преднапряженного каната (рис. 9). Целевое количество циклов нагружения составило 50 циклов, после чего образцы были доведены до разрушения.

Рисунок 9 - Пример образца при испытании
Значение предварительного напряжения арматуры относительно нормативного сопротивления каната растяжению, принято равным значению, при котором в растянутой (верхней) зоне бетон достигает предельного значения прочности на растяжение, то есть:
При замене получаем:
Нормативное сопротивление каната Rsn=1400 МПа, следовательно, относительное предварительное напряжение составит 554/1400=0,39.
Потерю напряжения выразим следующим образом:
где n — количество проволок в канате.
Тогда в момент времени t потерю предварительного напряжения можно выразить как функцию уменьшения площади сечения каната в каждый момент времени:
где A(t) — площадь сечения каната, поврежденного коррозией по (13).
Подобная методика и последовательность экспериментальных исследований позволяет:
1. Получить численные значения предельных нагрузок железобетонных балок с различной степенью коррозии преднапряженного каната при циклических нагружениях.
2. Определить изменения прогибов железобетонных балок в зависимости от степени коррозии преднапряженного каната.
3. Исследовать процессы деформирования и разрушения балок с корродированным канатом, выявить характер распространения трещин и потери несущей способности.
4. Определить снижение прочности и изменения механических характеристик преднапряженного каната в условиях коррозионного воздействия.
5. Исследовать коэффициент снижения прочности преднапряженного каната и влияние его деградации на общее напряженно-деформированное состояние балок.
6. Построить графики (напряжение — деформация) для преднапряженного каната с различной степенью коррозии при циклических нагрузках.
7. Построить графики N–f (нагрузка — прогиб) для железобетонных балок с разной степенью коррозии преднапряженного каната.
8. Исследовать распространение коррозии внутри преднапряженного каната, определить скорость разрушения проволок и влияние коррозии на сцепление арматуры с бетоном.
Эксперимент был выполнен в испытательной лаборатории Института промышленного и гражданского строительства ФГБОУ Национального исследовательского «Московского Государственного Строительного Университета» с использованием установок:
1. Instron 8802 — для динамических нагружений.
2. National Instruments LabVIEW 2010 — для регистрации деформаций при нагружениях.
3. Основные результаты
Предварительные расчеты показали, что стабильное решение численной модели выполняется при относительном предварительном напряжении каната 0,343, что соответствует растягивающему напряжению 480 МПа.
Выполнены расчеты трех типов моделей балок с различными параметрами, а именно:
– Балка без предварительного напряжения и коррозионных повреждений (№ 1);
– Балки идентичные экспериментальным образцам, имеющие процент коррозионных повреждений 0, 10%, 20% и соответствующие им потери предварительного напряжения 0, 5%, 8% (№ 2–№ 4);
– Балки с увеличенным относительно экспериментальных элементов коррозионным повреждением от 30% до 60% и соответствующие им потери предварительного напряжения от 11% до 20% (№ 5–№ 8).
Результаты выполненных расчетов представлены в таблице 1.
Таблица 1 - Результаты численных исследований экспериментальных балок
№ | % от Rsn | Преднап. c учетом потерь, МПа | As, см2 | Корр. повр., % | Потер. преднапр, % | Выгиб, см | Прогиб, см | σs, МПа | N, Н |
1 | 0 | 0 | 0.93 | 0 | 0 | 0 | 13,05 | 1332,6 | 81016 |
2 | 34,3 | 480 | 0,93 | 0 | 0 | 0,465 | 7,07 | 1401 | 90832 |
3 | 32,5 | 456 | 0,837 | 10 | 5 | 0,393 | 7,32 | 1401 | 83811 |
4 | 31,5 | 441,6 | 0,744 | 20 | 8 | 0,339 | 7,38 | 1403,9 | 76567 |
5 | 30,5 | 427,2 | 0,651 | 30 | 11 | 0,291 | 7,51 | 1403,7 | 68088 |
6 | 29,4 | 412,8 | 0,558 | 40 | 14 | 0,243 | 6,32 | 1401,3 | 58681 |
7 | 28,4 | 398,4 | 0,465 | 50 | 17 | 0,200 | 5,89 | 1404,7 | 50018 |
8 | 27,4 | 384 | 0,372 | 60 | 20 | 0,158 | 5,65 | 1404,1 | 40821 |
Примечание: Аs – площадь коррозионно-поврежденной арматуры; σs – напряжения в арматуре при достижении предельной нагрузки в модели; N – предельные усилия в модели; % от Rsn – значение предварительного напряжения относительно Rsn=1400 МПа
По результатам расчета численных моделей можно сделать вывод, что достижение предельной нагрузки обуславливается достижением условной площадки текучести каната.
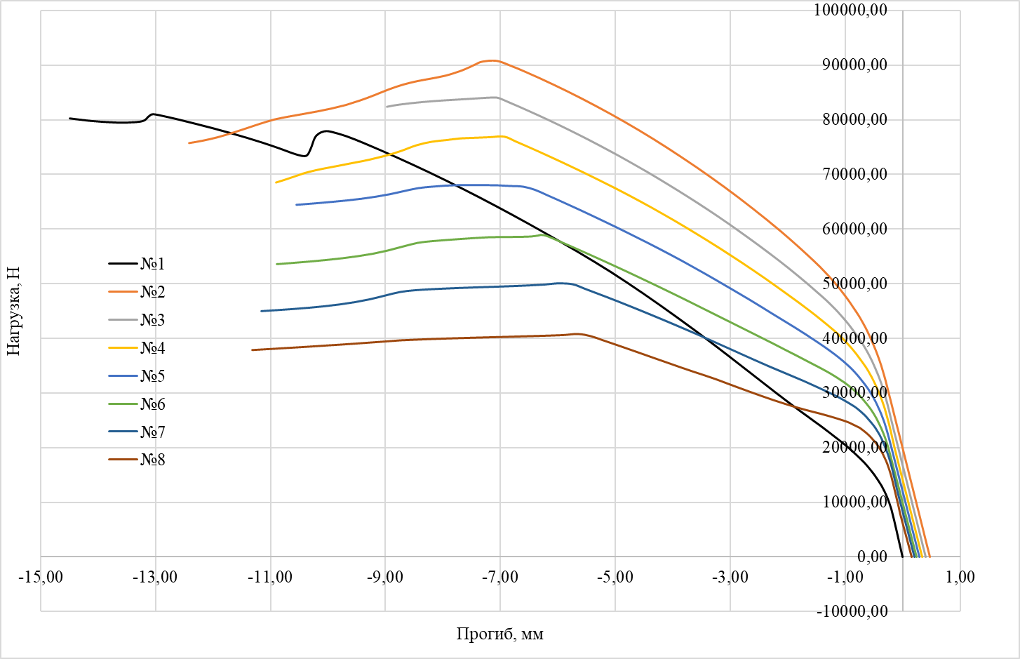
Рисунок 10 - График зависимости N–f различных моделей балок
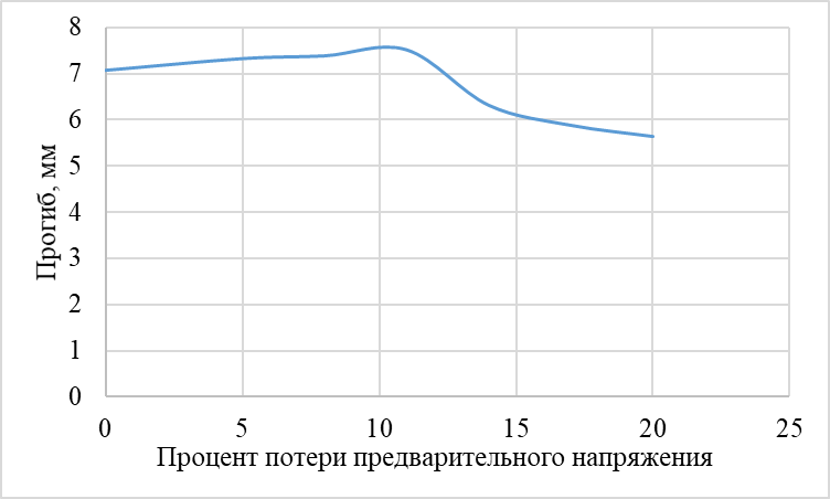
Рисунок 11 - График изменения прогиба балок в зависимости от процента потерь предварительного напряжения
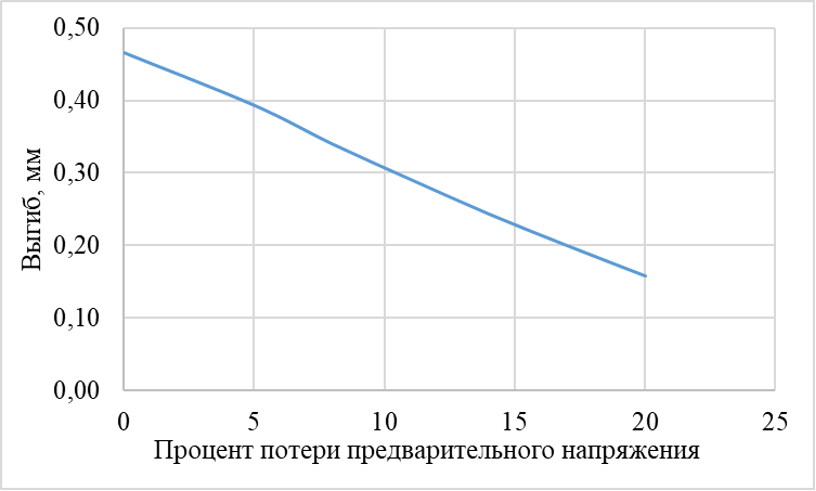
Рисунок 12 - График изменения выгиба балок в зависимости от процента потерь предварительного напряжения
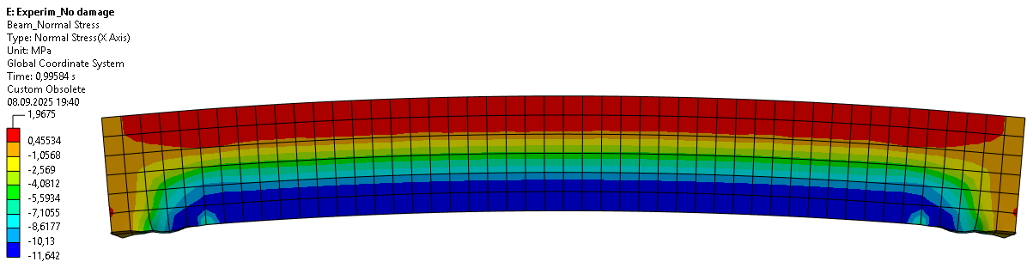
Рисунок 13 - Нормальные напряжения в балки после предварительного напряжения
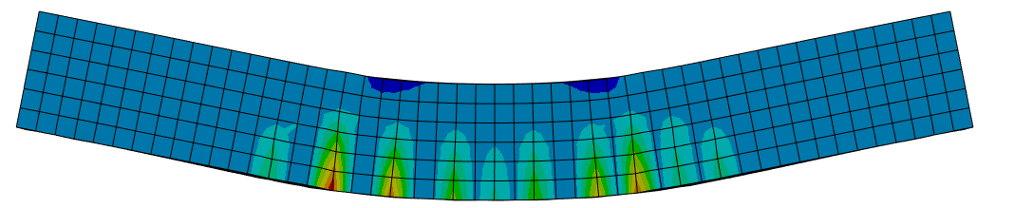
Рисунок 14 - Расположение трещин в балки после достижения предельной нагрузки

Рисунок 15 - Разрушение образцов
Сравнение разрушающей нагрузки образцов, полученной при проведении экспериментальных испытаний, со значениями предельной нагрузки, полученной в программном комплексе Ansys и представлены в таблице 2.
Таблица 2 - Результаты численных исследований балок
№ | Экспериментальная разрушающая нагрузка, кН | Разрушающая нагрузка в Ansys, кН | Сравнение, % |
1 | 90,8 | 81,3 | 89,51 |
2 | 83,8 | 73,9 | 88,17 |
3 | 76,6 | 65,5 | 85,55 |
Полученная достоверная сходимость между численными расчетами и результатами экспериментальных исследований, позволяет выполнить расчет полноразмерной предварительно напряженной подкрановой балки и оценить ее напряженно-деформированное состояние при коррозионных повреждениях стальных канатов с потерей предварительного напряжения.
Рассматриваемая балка таврового сечения со сжатой полкой в сжатой зоне длиной 12,0 м, высотой 1,2 м, шириной и высотой полки 0,65 м и 0,18 м соответственно. Армированная продольной арматурой из канатов К7 с условным пределом текучести Rsn=1400 МПа, диметр стержней принят 15,2 мм (As=139 мм2). В нижней зоне балки установлено шесть стержней, в верхней зоне четыре стержня (рис. 16).
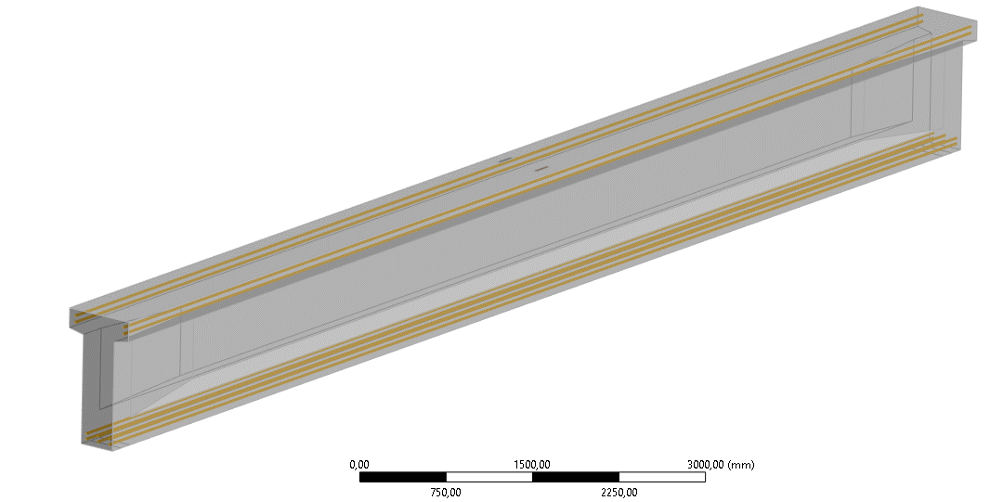
Рисунок 16 - Общий вид балки
Рисунок 17 - Триангуляция балки
Нагружение выполнялось в срединную часть балки через две металлические закладные детали.
Уменьшение площади сечения каната и потеря предварительного напряжения принималась аналогичной, как и в экспериментальных исследованиях. В таблице 3 приведены результаты численного исследования балки.
Таблица 3 - Результаты численных исследований полноразмерных балок
№ | % от Rsn | Преднап. c учетом потерь, МПа | As, см2 | Корр. повр., % | Потер. преднапр, % | Выгиб, см | Прогиб, см | σs, МПа | N, Н |
1 | 0 | 0 | 8,34 | 0 | 0 | 0 | 15,02 | 437,4 | 77993 |
2 | 90 | 1260 | 8,34 | 0 | 0 | 1,6300 | 41,77 | 1401 | 235790,0 |
3 | 85,5 | 1197 | 7,506 | 10 | 5 | 1,2568 | 40,481 | 1403 | 213090,0 |
4 | 82,8 | 1159,2 | 6,672 | 20 | 8 | 0,9384 | 40,54 | 1402 | 194080,0 |
6 | 80,1 | 1121,4 | 5,838 | 30 | 11 | 0,63412 | 38,49 | 1401 | 169580,0 |
7 | 77,4 | 1083,6 | 5,004 | 40 | 14 | 0,3438 | 39,92 | 1404 | 150720,0 |
8 | 74,7 | 1045,8 | 4,17 | 50 | 17 | 0,07 | 38,28 | 1405 | 127570,0 |
9 | 72 | 1008 | 3,336 | 60 | 20 | 0,05 | 17,84 | 1326 | 89986,0 |
Примечание: Аs – площадь коррозионно-поврежденной арматуры; σs – напряжения в арматуре при достижении предельной нагрузки в модели; N – предельные усилия в балке; % от Rsn – значение предварительного напряжения относительно Rsn=1400 МПа
На рисунках 18 и 19 представлены деформации, возникающие в бетоне при достижении предельной нагрузки в балке.
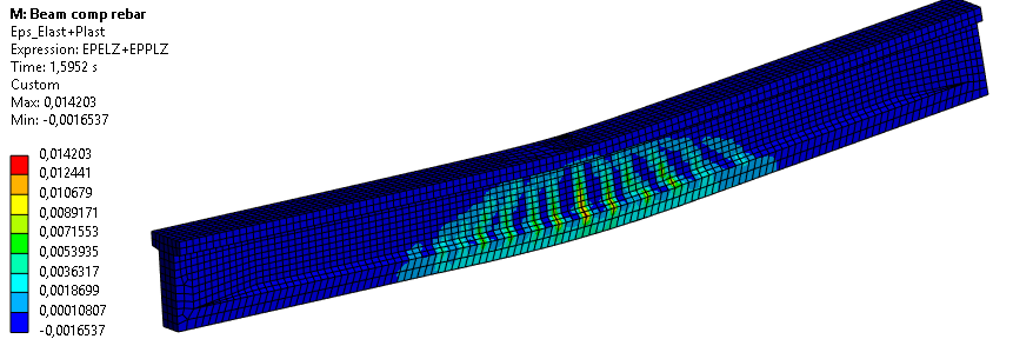
Рисунок 18 - Возникающие деформации в бетоне при достижении предельной нагрузки в балке
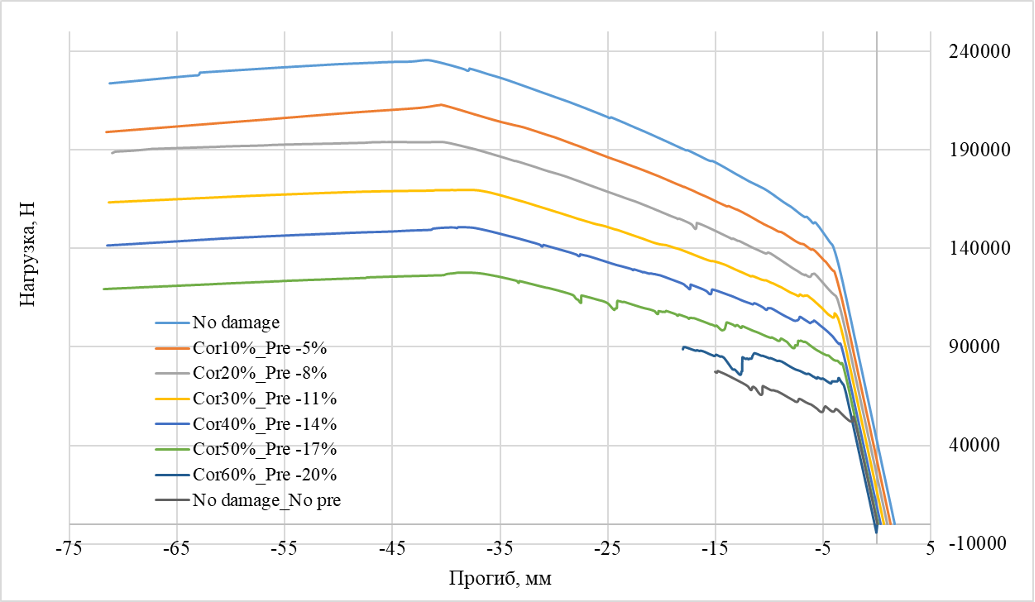
Рисунок 19 - График возникающих деформаций в бетоне при достижении предельной нагрузки в балке
4. Заключение
Сравнительный анализ несущей способности в экспериментальных образцах с результатами численного расчета имеет достаточно хорошую сходимость, что показывает корректность принятых прочностных и жесткостных характеристик материалов, типов конечных элементов, граничных условий, использование моделей поведения бетона и арматуры и как результат позволяют достоверно проводить численные исследования данных моделей изменяя тип и степень предварительного напряжения каната.
Проведенные комплексные экспериментальные и численные исследования позволили получить следующие новые научные результаты:
1. Разработана и верифицирована детализированная конечно-элементная модель, позволяющая адекватно оценивать снижение несущей способности и изменение характера работы предварительно напряженных изгибаемых элементов при коррозионном повреждении арматуры. Новизна модели заключается в комплексном учете:
– Уменьшения площади сечения арматуры.
– Снижения уровня предварительного напряжения как следствия коррозии.
2. Установлен и количественно оценен нелинейный характер влияния степени коррозии на деформативность. Получены данные, показывающие, что при коррозии до 30% прогибы балок увеличиваются, а при дальнейшем развитии повреждений (40–60%) наблюдается их аномальное уменьшение, что свидетельствует о переходе к хрупкой форме разрушения и потере эксплуатационной пригодности элемента.
3. Результаты численного исследования показывают, что достижение предельной нагрузки обуславливается достижением условной площадки текучести, за исключением балки не имеющей предварительного напряжения и модели, имеющей 60% коррозионного повреждения арматуры. Следовательно, можно сделать вывод, что значительные коррозионные повреждения и потеря предварительного напряжения арматуры приводят к смене типа разрушения, то есть с пластического к хрупкому.
