ОПРЕДЕЛЕНИЕ ТЕРМОФЛУКТУАЦИОННЫХ КОНСТАНТ ОБОБЩЕННОГО УРАВНЕНИЯ ЖУРКОВА МНОГОСЛОЙНЫХ ПЛАСТИКОВЫХ СЭНДВИЧ-ПАНЕЛЕЙ РАЗЛИЧНЫМИ СПОСОБАМИ
ОПРЕДЕЛЕНИЕ ТЕРМОФЛУКТУАЦИОННЫХ КОНСТАНТ ОБОБЩЕННОГО УРАВНЕНИЯ ЖУРКОВА МНОГОСЛОЙНЫХ ПЛАСТИКОВЫХ СЭНДВИЧ-ПАНЕЛЕЙ РАЗЛИЧНЫМИ СПОСОБАМИ
Аннотация
Для прогнозирования долговечности твердых тел необходимо определить термофлуктуационные константы обобщенного уравнения Журкова. В классическом случае физический смысл определяемых четырех констант следующий: период колебания кинетической единицы, начальная энергия активации процесса разрушения, температура существования твердого тела и структурно-механическая константа. В настоящее время существует несколько методик по их определению. В работе термофлуктуационные константы обобщенного уравнения Журкова определены для многослойных пластиковых сэндвич-панелей при поперечном изгибе двумя способами. По результатам исследования делается вывод о сходимости результатов определения термофлуктуационных констант обобщенного уравнения Журкова, полученных различными способами.
1. Введение
В настоящее время прогнозирование долговечности твердых тел ведется в рамках термофлуктуационной концепции разрушения и деформирования твердых тел, в основе которой лежит представление о том, что решающая роль в процессе разрушения принадлежит тепловому движению кинетических единиц , , , , . Основоположником концепции является Журков Серафим Николаевич, который дал трактовку физического смысла констант, входящих в уравнение, впоследствии получившее его имя (уравнение Журкова) . Развитие концепция получила в работах Регель В.Р., Томашевского Э.Е., Слуцкера А.И. и ряда других видных ученых Советского Союза . Так, Ярцевым В.П. и Ратнером С.Б. уравнение Журкова было модифицировано путем добавления четвертой константы (температуры существования твердого тела) . Поученное уравнение получило название обобщенного уравнения Журкова, имеющего следующий вид:
Для определения долговечности материала для него необходимо установить четыре термофлуктуационные константы, которые определяются на основе экспериментальных данных зависимости долговечности от напряжения, действующего в материале, и температуры окружающей среды. В настоящей работе термофлуктуационные константы обобщенного уравнения Журкова определены для многослойных пластиковых сэндвич-панелей при поперечном изгибе двумя разными методами: классический метод и метод эталонного пучка .
2. Методы и принципы исследования
Испытания проводились на образцах-балочках прямоугольного сечения размерами bхh=20х8,8 мм. Длина образцов составляла 12 см. Для испытаний на поперечный изгиб использовался шестипозиционный стенд (рисунок 1), состоящий из рамы 1, выполненной из уголков, на опорной площадке которой установлены два стержня 3 диаметром 6 мм. Образец 2 помещался широкой стороной на опорные стержни и нагружался с помощью грузового устройства 4. Расстояние между опорными стержнями составляло 10 см. Расчетная схема – однопролетная балка на двух опорах. Нагрузка прикладывалась сосредоточено по центру.
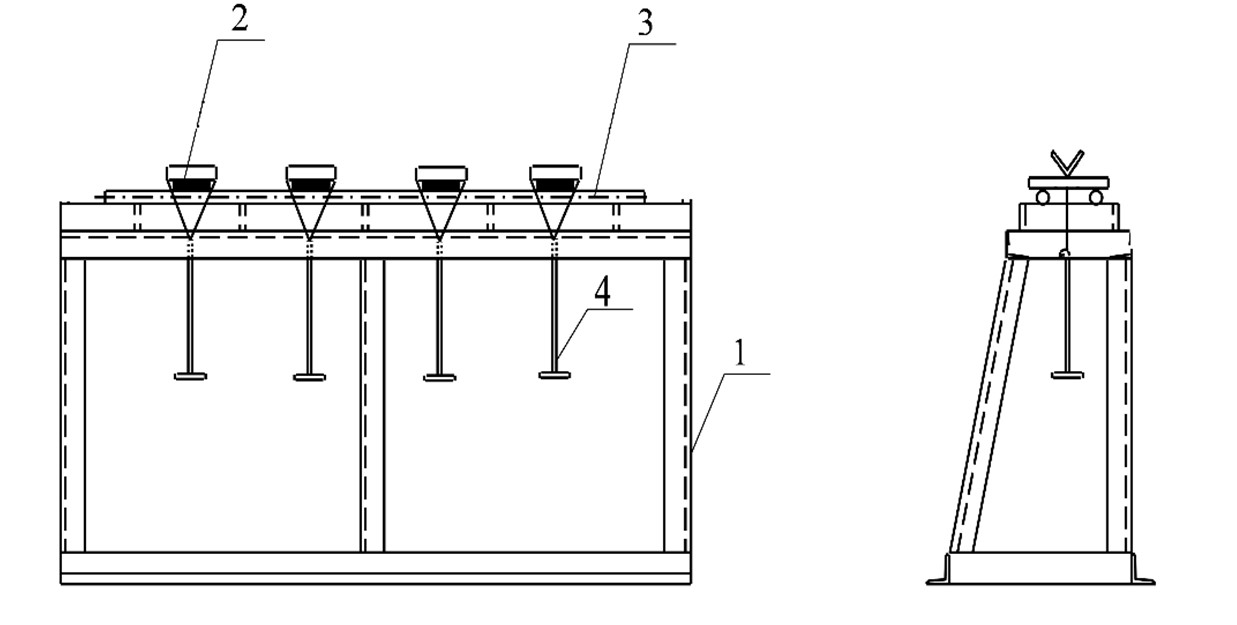
Рисунок 1 - Шестипозиционный стенд для испытаний на поперечный изгиб
Примечание: 1 – корпус стенда; 2 – конусообразные держатели образцов; 3 – опоры для образцов (упоры); 4 – испытуемые образцы
3. Основные результаты
Полученные экспериментальные данные зависимости долговечности (логарифм долговечности) от действующих в материале напряжений и температуры окружающей среды сведены в таблицу 1.
Таблица 1 - Экспериментальные данные зависимости долговечности от напряжения и температуры многослойных пластиковых сэндвич-панелей при поперечном изгибе
| T = 30 ○С | ||||
σ=2,51 МПа | σ=2,46 МПа | σ=2,40 МПа | σ=2,30 МПа | σ=2,22 МПа | |
lgԏ | 0,000 | 1,431 | 0,000 | 2,843 | 0,301 |
0,000 | 1,000 | 0,845 | 0,903 | 3,338 | |
0,000 | 0,301 | 0,000 | 2,705 | 2,468 | |
0,602 | 0,000 | 0,845 | 2,430 | 1,079 | |
0,000 | 0,000 | 0,699 | 0,477 | 0,699 | |
0,477 | 0,602 | 0,000 | 1,204 | 4,048 | |
0,000 | 2,330 | 2,664 | 2,307 | 2,505 | |
0,000 | 1,959 | 1,000 | 0,477 | 3,278 | |
| T = 40 ○С | ||||
σ=2,45 МПа | σ=2,35 МПа | σ=2,24 МПа | σ=2,17 МПа | σ=2,09 МПа | |
lgԏ | 0,000 | 0,000 | 2,664 | 2,348 | 3,439 |
0,301 | 1,973 | 1,380 | 2,104 | 1,763 | |
1,041 | 1,176 | 0,301 | 1,301 | 2,373 | |
0,301 | 0,301 | 0,000 | 1,924 | 2,173 | |
0,699 | 0,000 | 0,000 | 2,068 | 0,477 | |
0,301 | 0,301 | 0,301 | 2,539 | 0,602 | |
0,301 | 0,000 | 0,778 | 0,477 | 1,447 | |
1,176 | 0,477 | 1,230 | 0,000 | 0,699 | |
| T = 50 ○С | ||||
σ=2,20 МПа | σ=2,06 МПа | σ=1,94 МПа | σ=1,85 МПа | σ=1,46 МПа | |
lgԏ | 0,477 | 0,000 | 1,000 | 2,664 | 1,380 |
0,000 | 1,000 | 2,714 | 0,699 | 0,000 | |
0,000 | 0,301 | 3,091 | 2,606 | 1,301 | |
0,000 | 0,000 | 0,477 | 2,400 | 0,301 | |
0,000 | 0,903 | 0,477 | 0,903 | 0,699 | |
0,000 | 1,732 | 2,250 | 1,342 | 1,279 | |
0,000 | 0,845 | 0,954 | 3,302 | 1,146 | |
1,398 | 1,301 | 0,301 | 1,322 | 2,569 | |
Полученные экспериментальные данные (таблица 1) были проверены на наличие грубых погрешностей по критерию Граббса. Также были найдены доверительные интервалы полученных экспериментальных значений. Полученные результаты средних значений и границы доверительного интервала сведены в таблицу 2.
Таблица 2 - Значения десятичного логарифма времени [с] при заданных напряжениях и температурах после статистической обработки данных
Напряжение (σ), МПа | Среднее значение логарифма долговечности и границы доверительного интервала при температуре | ||||||||||
30 °C | 40 °C | 50 °C | |||||||||
Н** | Ср* | В*** | Н** | Ср* | В*** | Н** | Ср* | В*** | |||
2,51 | -0,285 | 0,135 | 0,555 | - | - | - | - | - | - | ||
2,46 | 0,166 | 0,953 | 1,740 | - | - | - | - | - | - | ||
2,45 | - | - | - | -0,023 | 0,515 | 1,053 | - | - | - | ||
2,40 | -0,144 | 0,484 | 1,112 | - | - | - | - | - | - | ||
2,35 | - | - | - | -0,172 | 0,529 | 1,229 |
|
|
| ||
2,30 | 0,830 | 1,668 | 2,507 | - | - | - | - | - | - | ||
2,24 | - | - | - | 0,035 | 0,832 | 1,628 | - | - | - | ||
2,22 | 1,236 | 2,215 | 3,194 | - | - | - | - | - | - | ||
2,20 | - | - | - | - | - | - | -0,325 | 0,068 | 0,461 | ||
2,17 | - | - | - | 0,793 | 1,595 | 2,397 | - | - | - | ||
2,09 | - | - | - | 0,773 | 1,622 | 2,470 | - | - | - | ||
2,06 | - | - | - | - | - | - | 0,102 | 0,760 | 1,419 | ||
1,94 | - | - | - | - | - | - | 0,528 | 1,408 | 22,88 | ||
1,85 | - | - | - | - | - | - | 1,088 | 1,905 | 2,722 | ||
1,76 | - | - | - | - | - | - | 0,343 | 1,084 | 1,826 | ||
Примечание: *Ср – средние значения величины десятичного логарифма времени в секундах; **Н – нижняя граница доверительного интервала; ***В – верхняя граница доверительного интервала
По приведенным в таблице 2 статически обработанным данным построен график в координатах «lgԏ – σ» (рисунок 2).
Из графика видно, что при исследуемых температурах зависимость долговечности (lgԏ) от напряжения (σ) подчиняется линейной зависимости, при этом температурные прямые сходятся в «прямой пучок», т.е. наблюдается схождение в полюс при предельно высокой температуре, что является классическим представлением термофлуктуационной теории для данного материала.
По графику (рисунок 2) можно определить, что точка полюса сходится по оси абсцисс σ = 2,75 МПа и по оси ординат lgԏ = - 1,38 с. Прямолинейная зависимость lgԏ = f(σ) при различных температурах описывается уравнениями, приведенными ниже:
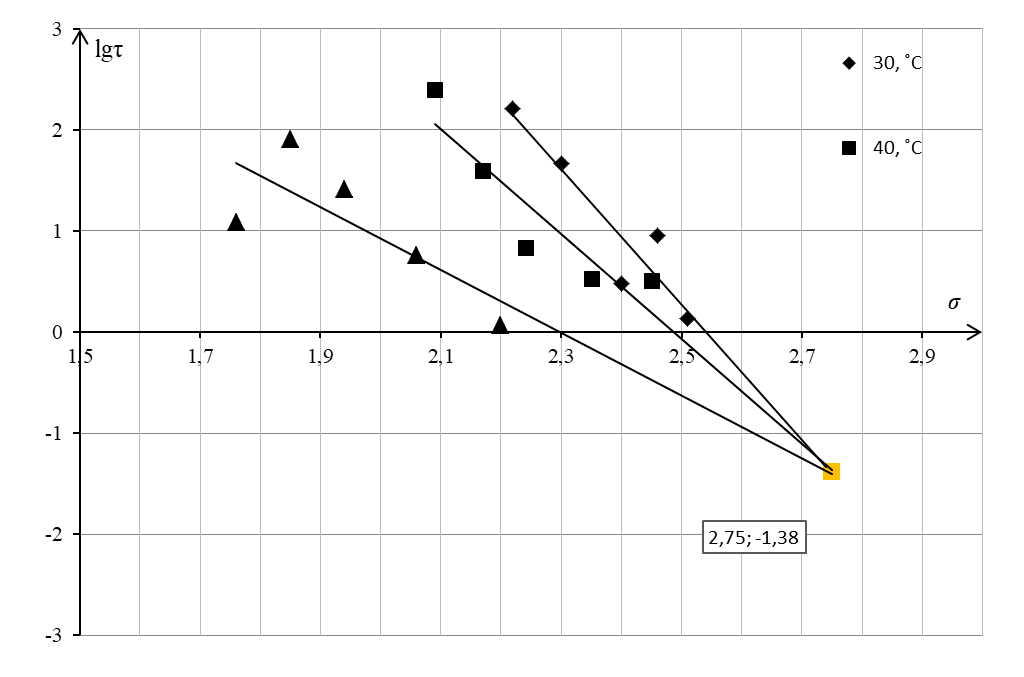
Рисунок 2 - Зависимость логарифма долговечности от напряжения для многослойных пластиковых сэндвич-панелей
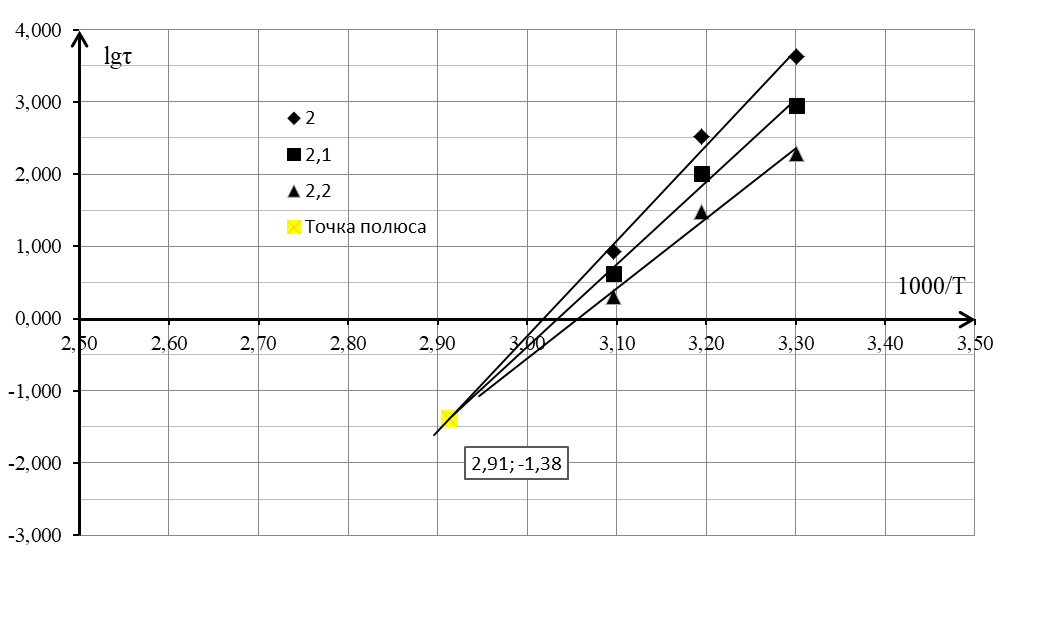
Рисунок 3 - Зависимость логарифма долговечности от обратной температуры увеличенной в 1000 раз для многослойных пластиковых сэндвич-панелей
Для каждой прямой графика «lgԏ – 1000/T», которая характеризует фиксированное значение напряжения, определялась энергия активации. Энергия активации для напряжения 2,0 МПа составляет U = 251,886 кДж/моль, для напряжения 2,1 МПа она составляет U = 218,244 кДж/моль и для напряжения 2,2 МПа – U = 184,603 кДж/моль. По найденным значениям строится прямая в координатах «U – σ» (рисунок 4). Данная прямая экстраполируется на ось ординат с целью определения начальной энергии активации. Таким образом, прямолинейная зависимость для образцов цельного сечения Uo = f(σ) описывается следующим уравнением:
Из данного уравнения определяются последние две константы Uo = 924,71 кДж/моль и ɣ = 336,41 кДж/(МПа×моль).
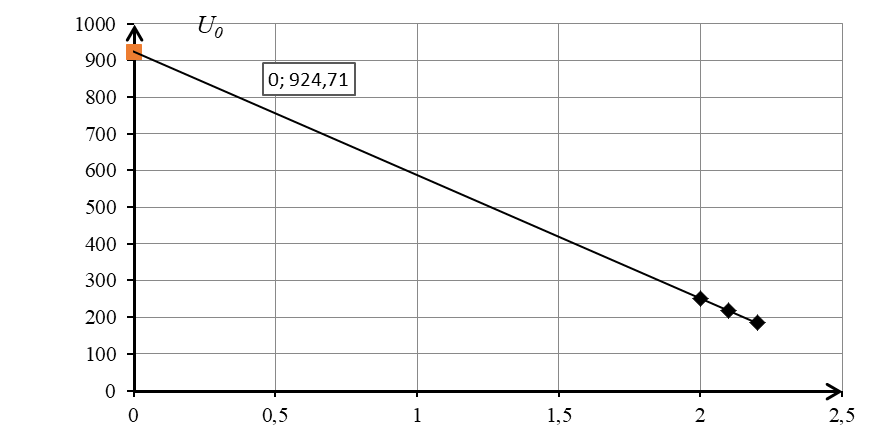
Рисунок 4 - Зависимость энергии активации процесса разрушения от напряжения для многослойных пластиковых сэндвич-панелей
Точка полюса (пересечение прямых температур (рисунок 2)) имеет координаты (2,75; -1,38). Следовательно, константа lgԏo, являющаяся ординатой точки полюса, равна -1,38.
Изменение угловых коэффициентов уравнения прямых температур (2), (3) и (4) описывается следующим уравнением:
тогда при a = 0, Tm = 343,24 К.
Согласно методу эталонного пучка, термофлуктуационная константа Uo определяется путем умножения значения эталонной константы на систему коэффициентов kσ и kk, а структурно-механическая константа ɣ определяется путем умножения эталонной константы на коэффициент kk.
Коэффициент kk = (-17,601)/(-2,619)=6,721, коэффициент kσ =2,75/10=0,275. Тогда U0 = 500∙6,721∙0,275=924,14 кДж/моль, а структурно-механическая константа ɣ = 50∙6,721=336,05 кДж/(МПа×моль).
4. Заключение
В итоге для многослойных пластиковых сэндвич-панелей классическим способом получены следующие термофлуктуационные константы обобщенного уравнения Журкова: lgԏ0 = -1,38 с, Tm = 343,64 К, U0 = 924,71 кДж/моль, ɣ = 336,41 кДж/(МПа×моль).
Для многослойных пластиковых сэндвич-панелей методом эталонного пучка получены следующие термофлуктуационные константы обобщенного уравнения Журкова: lgԏ0 = -1,38 с, Tm = 343,24 К, U0 = 924,14 кДж/моль, ɣ = 336,05 кДж/(МПа×моль).
Проведенные исследования на примере многослойных пластиковых сэндвич-панелей показали высокую сходимость двух методов определения термофлуктуационных констант обобщенного уравнения Журкова.
