EXPERIMENTAL AND STATISTICAL MODEL OF CHANGES IN THE STRENGTH OF HYDRAULIC ENGINEERING CONCRETES USING COMPLEX MODIFYING ADDITIVES
EXPERIMENTAL AND STATISTICAL MODEL OF CHANGES IN THE STRENGTH OF HYDRAULIC ENGINEERING CONCRETES USING COMPLEX MODIFYING ADDITIVES
Abstract
The article considers a three-factor mathematical planned experiment. When calculating the dependence on variable factors (X1; X2; X3) for the compressive strength of cement stone in 28 days, the "PlanExp B-D13" software package was used. The maximum strength parameters of the obtained hydraulic engineering concretes are determined. A graphical interpretation of the regression equation from the acting factors is performed. The significance of the coefficients of the equations of the mathematical model was checked using the Student's criterion. The adequacy of the equation of the mathematical model was checked using the Fisher criterion. Acceptable values of the variable factors were determined using compromise values by analyzing graphical interpretations of the regression equation, which characterizes the change in values of compressive strength at the age of 28 days.
The aim of the work is to optimise the compressive strength performance of hydraulic engineering concrete modified with microsilica using sulphoferritic type admixture.
1. Введение
Использование современных вычислительных математических программных комплексов в области анализа данных и построения регрессионных моделей позволяет оптимизировать процесс исследования и минимизировать затраты материальных и временных ресурсов, открывать возможности для автоматизации расчётов, обработки больших объёмов данных, строить различные типы регрессионных моделей, оценивать их качества, прогнозировать результаты и визуализировать полученные данные
, , , . Применение программных комплексов позволяет сократить материальные затраты на проведение экспериментов, уменьшить временные затраты на обработку данных, повысить точность результатов и упростить процесс анализа и интерпретации данных, что критически важно при работе со сложными системами, где необходимо учитывать множество переменных и проводить комплексный анализ для получения достоверных результатов .При оптимизации физико-механических параметров тяжелых гидротехнических бетонов используют определенные математические подходы, которые условно подразделяются на несколько групп:
1) вероятно-статистические методы, включающие использование общей теории вероятности, описательной статистики, выборочного метода и проверку статистических гипотез, дисперсного и регрессионного анализа, математической теории экспериментов и т.д.
;2) методы исследования операций, которые включают линейное, нелинейное и динамическое программирование, теорию игр, теорию массового обслуживания, теорию графов и сетей и т.п.
, ;3) методы математического анализа, включающие дифференциальное, интегральное и векторное исчисление, дифференциальные уравнения, в том числе уравнения математической физики, используемые для составления и расчета математических моделей на основе определенных предпосылок о физикохимии исследуемых процессов
;4) использование искусственного интеллекта
, , .В работе использовался трехфакторный планированный эксперимент . В качестве программно-алгоритмического средства обработки данных принят "PlanExp B-D13" . Данная программа обладает алгоритмом расчета, который включает в себя основные процедуры
, , :1) расчет коэффициентов функции отклика;
2) статистической обработка уравнений математической модели.
Основные вычисления, приведенные в работе, рассчитываются циклично, что может позволить перестроить уравнение математической модели моментально, при изменении параметров входных данных
, , .Целью работы является оптимизация показателей прочности при сжатии гидротехнического бетона, модифицированного микрокремнеземом, с использованием добавки сульфоферритного типа.
2. Основные результаты
В качестве участвующих в планировании эксперимента переменных факторов на 1 м3 тяжелого гидротехнического бетона принимаем:
• Х1 — портландцемент типа ЦЕМ I 42,5Н, выпускаемый АО «ЛИПЕЦКЦЕМЕНТ», кг.;
• Х2 — 10% микрокремнезем МК-85+ добавка сульфоферритного типа (изменяется от 12,5 до 17,5%) от массы портландцемента;
• Х3 — количество суперпластификатора для бетона BASF MasterGlenium ACE 430 – % от массы портландцемента;
Выходным параметром при планировании эксперимента выбран:
• Y1 — прочность на сжатие при выдерживании в нормальных условиях твердения в возрасте 28 суток, МПа.
Для получения результатов графической интерпретации использовался программный комплекс "Microsoft Excel".
В таблице 1 представлены факторы и интервалы их варьирования.
Таблица 1 - Факторы и интервалы их варьирования
Фактор | Нижний уровень (-1) | Основной уровень (0) | Верхний уровень (+1) | Интервал варьирования | Наименование фактора |
Х1: | 185 | 240 | 295 | 55 | Портландцемент типа ЦЕМ I 42,5Н, кг. |
Х2: | 22,5 | 25 | 27,5 | 2,5 | 10% микрокремнезем МК-85+ добавка сульфоферритного типа (изменяется от 12,5 до 17,5 %) от массы ПЦ |
Х3: | 1 | 1,5 | 2 | 0,5 | BASF MasterGlenium ACE 430, % от mц |
В таблице 2 план эксперимента и выходные параметры опытов.
Таблица 2 - План эксперимента и выходные параметры опытов
Номер опыта (u) | Матрица планирования | Натуральные значения переменных | Выходной параметр (Прочность в 28 суток, МПа) | ||||||
Х1 | Х2 | Х3 | Портландцемент типа ЦЕМ I 42,5Н, кг | 10% микрокремнезем МК-85 + добавка сульфоферритного типа (изменяется от 12,5 до 17,5 %) от mц | BASF MasterGlenium ACE 430, % от mц | y(u, 1) | y(u, 2) | y(u, 3) | |
1 | -1 | -1 | -1 | 185 | 22,5 | 1 | 56,1 | 45,8 | 47,6 |
2 | +1 | -1 | -1 | 295 | 22,5 | 1 | 40,0 | 43,1 | 53,5 |
3 | -1 | +1 | -1 | 185 | 27,5 | 1 | 46,7 | 43,8 | 61,7 |
4 | -1 | -1 | +1 | 185 | 22,5 | 2 | 52,8 | 61,6 | 57,0 |
5 | -1 | 0,19 | 0,19 | 185 | 25,5 | 1,6 | 65,3 | 64,9 | 64,6 |
6 | 0,19 | -1 | 0,19 | 250,5 | 22,5 | 1,6 | 55,0 | 48,7 | 58,0 |
7 | 0,19 | 0,19 | -1 | 250,5 | 25,5 | 1 | 51,9 | 53,2 | 60,1 |
8 | -0,29 | +1 | +1 | 224,1 | 27,5 | 2 | 49,6 | 53,7 | 52,2 |
9 | +1 | -0,29 | +1 | 295 | 24,3 | 2 | 62,6 | 68,5 | 59,5 |
10 | +1 | +1 | -0,29 | 295 | 27,5 | 1,4 | 52,9 | 46,3 | 54,3 |
Коэффициенты уравнения математической модели представлены в таблице 3.
Таблица 3 - Коэффициенты уравнения математической модели
b0 | b1 | b2 | b3 | b11 | b12 | b13 | b22 | b23 | b33 | |
Rсж.28 | 61,914 | -1,447 | -0,75 | 3,326 | 1,677 | -0,099 | 0,796 | -9,371 | -1,113 | -2,89 |
Значимость коэффициентов уравнений математической модели проверяется при помощи критерия Стьюдента (табл. 4). Адекватность уравнения математической модели проверяется по критерию Фишера.
Таблица 4 - Критерии Стьюдента и значимость коэффициентов математической модели
b0 | b1 | b2 | b3 | b11 | b12 | b13 | b22 | b23 | b33 | |
t-критерий | 12,616 | 0,689 | 0,357 | 1,583 | 0,413 | 0,04 | 0,318 | 2,308 | 0,444 | 0,712 |
Значимость | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
Примечание: 1/0 – значимый/незначимый
Дисперсия адекватности математической модели: 54,188.
Число степеней свободы при значимых коэффициентах: 8.
Табличное значение критерия Фишера: 2,45.
Расчетное значение критерия Фишера: 1,95.
Зависимость от переменных факторов (Х1; Х2; Х3) для прочности при сжатии цементного камня в 28 суток:
Зависимость переменных факторов для прочности показывает, что присутствие знаков «минус» при факторах Х1; Х2 и Х3 приводит к понижению прочности гидротехнического бетона. Положительная зависимость факторов Х1 и Х3 показывает повышение прочности при сжатии с единовременным увеличением вводимого суперпластификатора "BASF MasterGlenium ACE 430", что приводит к увеличению прочности гидротехнического бетона при сжатии.
В связи с тем, что для графической интерпретации функции трех переменных требуется четырехмерное пространство, поэтому для упрощения работы, а также удобством в будущем с уравнениями регрессии, функцию трех переменных требуется перевести в функцию двух переменных, при этом каждый раз принимая в виде константы один из используемых факторов. Основываясь на результатах уравнения регрессии для прочности при сжатии на 28-й день выдержки образцов в нормальных условиях, с использованием программного обеспечения "Microsoft Excel" были созданы графические представления уравнения регрессии, отражающего взаимосвязь между пределом прочности при сжатии и возрастом образцов (рис. 1–3). Каждый фактор, участвующий в построении графиков, фиксировался на нулевом уровне. Приемлемые значения варьируемых факторов определялись при помощи поиска компромиссных значений с помощью анализа графических интерпретации уравнения регрессии, характеризующего изменение предела прочности при сжатии в возрасте 28 суток.
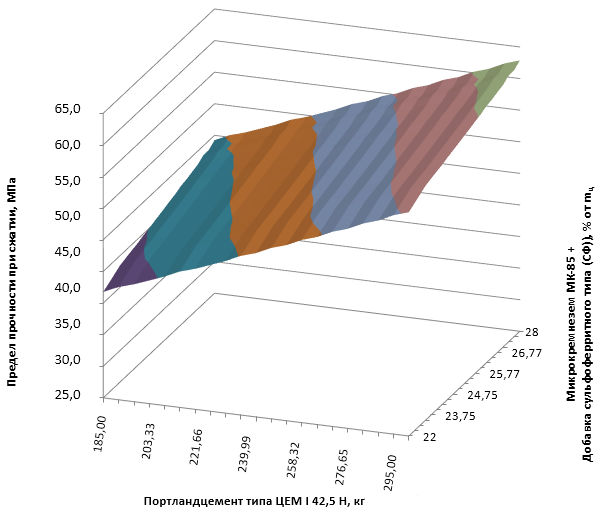
Рисунок 1 - Графическая интерпретация уравнения регрессии, характеризующего изменение предела прочности при сжатии в возрасте 28 суток от действующих факторов (Х1; Х2)
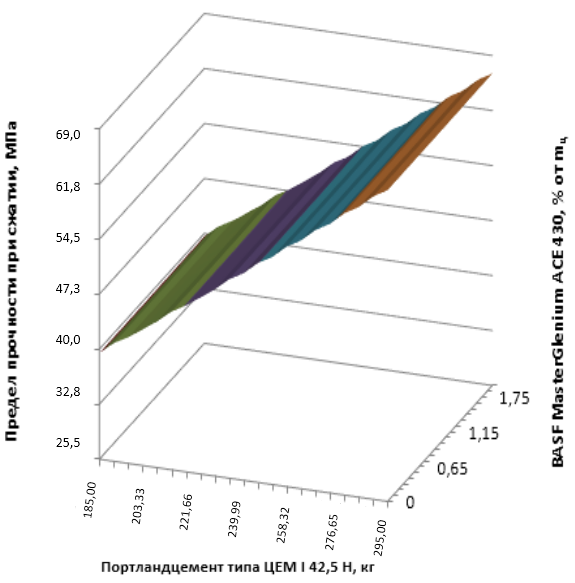
Рисунок 2 - Графическая интерпретация уравнения регрессии, характеризующего изменение предела прочности при сжатии в возрасте 28 суток от действующих факторов (Х1, Х3)

Рисунок 3 - Графическая интерпретация уравнения регрессии, характеризующего изменение предела прочности при сжатии в возрасте 28 суток от действующих факторов (Х2; Х3)
3. Заключение
По результатам проведенного математического планированного эксперимента, установлено, что требуемые показатели предела прочности при сжатии гидротехнических бетонов достигаются с использованием портландцемента типа ЦЕМ I 42,5Н в количестве 240 кг., 10% микрокремнезем МК-85 + добавка сульфоферритного типа 11% от массы портландцемента, суперпластификатора "BASF MasterGlenium ACE 430" 1,5% от массы цемента.
