DETERMINATION OF THERMOFLUCTUATION CONSTANTS OF THE GENERALISED ZURKOV EQUATION OF MULTILAYER PLASTIC SANDWICH PANELS BY DIFFERENT METHODS
DETERMINATION OF THERMOFLUCTUATION CONSTANTS OF THE GENERALISED ZURKOV EQUATION OF MULTILAYER PLASTIC SANDWICH PANELS BY DIFFERENT METHODS
Abstract
To predict the durability of solid bodies, it is necessary to determine the thermofluctuation constants of the generalized Zhurkov equation. In the classical case, the physical meaning of the four constants to be determined is as follows: the period of oscillation of the kinetic unit, the initial activation energy of the destruction process, the existence temperature of the solid, and the structural-mechanical constant. Currently, there are several techniques for their determination. In this work, the thermofluctuation constants of the generalized Zhurkov equation are determined for multilayer plastic sandwich panels in transverse bending by two methods. According to the results of the study, it is concluded that the results of determining the thermofluctuation constants of the generalized Zhurkov equation obtained by different methods converge.
1. Введение
В настоящее время прогнозирование долговечности твердых тел ведется в рамках термофлуктуационной концепции разрушения и деформирования твердых тел, в основе которой лежит представление о том, что решающая роль в процессе разрушения принадлежит тепловому движению кинетических единиц , , , , . Основоположником концепции является Журков Серафим Николаевич, который дал трактовку физического смысла констант, входящих в уравнение, впоследствии получившее его имя (уравнение Журкова) . Развитие концепция получила в работах Регель В.Р., Томашевского Э.Е., Слуцкера А.И. и ряда других видных ученых Советского Союза . Так, Ярцевым В.П. и Ратнером С.Б. уравнение Журкова было модифицировано путем добавления четвертой константы (температуры существования твердого тела) . Поученное уравнение получило название обобщенного уравнения Журкова, имеющего следующий вид:
Для определения долговечности материала для него необходимо установить четыре термофлуктуационные константы, которые определяются на основе экспериментальных данных зависимости долговечности от напряжения, действующего в материале, и температуры окружающей среды. В настоящей работе термофлуктуационные константы обобщенного уравнения Журкова определены для многослойных пластиковых сэндвич-панелей при поперечном изгибе двумя разными методами: классический метод и метод эталонного пучка .
2. Методы и принципы исследования
Испытания проводились на образцах-балочках прямоугольного сечения размерами bхh=20х8,8 мм. Длина образцов составляла 12 см. Для испытаний на поперечный изгиб использовался шестипозиционный стенд (рисунок 1), состоящий из рамы 1, выполненной из уголков, на опорной площадке которой установлены два стержня 3 диаметром 6 мм. Образец 2 помещался широкой стороной на опорные стержни и нагружался с помощью грузового устройства 4. Расстояние между опорными стержнями составляло 10 см. Расчетная схема – однопролетная балка на двух опорах. Нагрузка прикладывалась сосредоточено по центру.
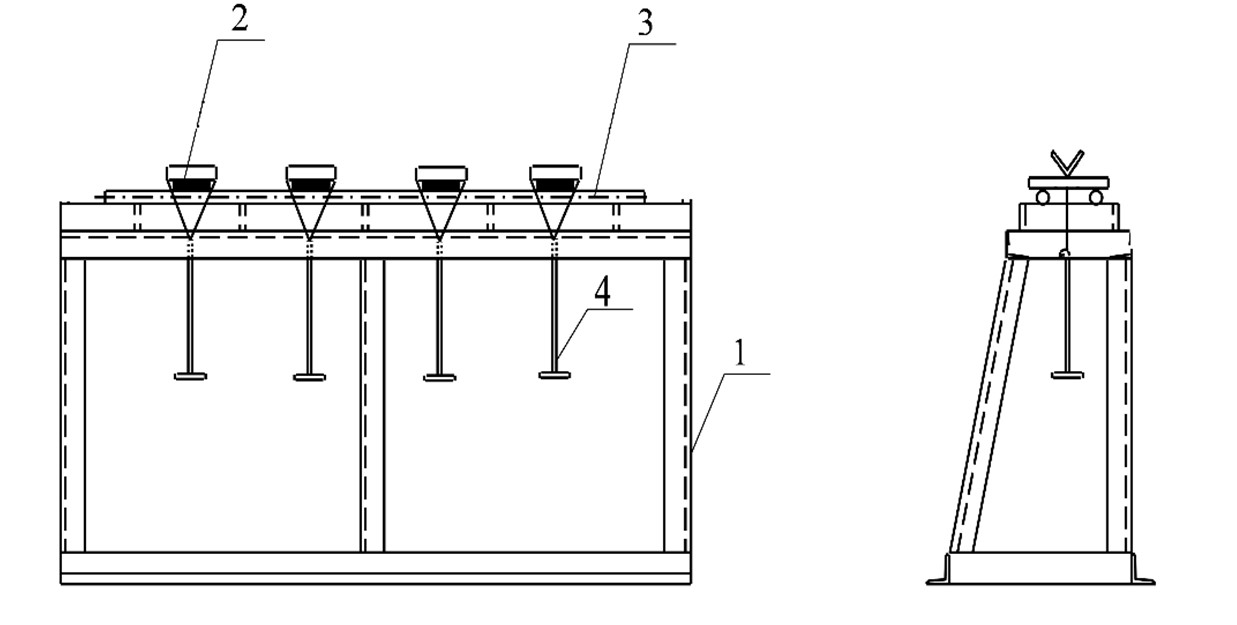
Рисунок 1 - Шестипозиционный стенд для испытаний на поперечный изгиб
Примечание: 1 – корпус стенда; 2 – конусообразные держатели образцов; 3 – опоры для образцов (упоры); 4 – испытуемые образцы
3. Основные результаты
Полученные экспериментальные данные зависимости долговечности (логарифм долговечности) от действующих в материале напряжений и температуры окружающей среды сведены в таблицу 1.
Таблица 1 - Экспериментальные данные зависимости долговечности от напряжения и температуры многослойных пластиковых сэндвич-панелей при поперечном изгибе
| T = 30 ○С | ||||
σ=2,51 МПа | σ=2,46 МПа | σ=2,40 МПа | σ=2,30 МПа | σ=2,22 МПа | |
lgԏ | 0,000 | 1,431 | 0,000 | 2,843 | 0,301 |
0,000 | 1,000 | 0,845 | 0,903 | 3,338 | |
0,000 | 0,301 | 0,000 | 2,705 | 2,468 | |
0,602 | 0,000 | 0,845 | 2,430 | 1,079 | |
0,000 | 0,000 | 0,699 | 0,477 | 0,699 | |
0,477 | 0,602 | 0,000 | 1,204 | 4,048 | |
0,000 | 2,330 | 2,664 | 2,307 | 2,505 | |
0,000 | 1,959 | 1,000 | 0,477 | 3,278 | |
| T = 40 ○С | ||||
σ=2,45 МПа | σ=2,35 МПа | σ=2,24 МПа | σ=2,17 МПа | σ=2,09 МПа | |
lgԏ | 0,000 | 0,000 | 2,664 | 2,348 | 3,439 |
0,301 | 1,973 | 1,380 | 2,104 | 1,763 | |
1,041 | 1,176 | 0,301 | 1,301 | 2,373 | |
0,301 | 0,301 | 0,000 | 1,924 | 2,173 | |
0,699 | 0,000 | 0,000 | 2,068 | 0,477 | |
0,301 | 0,301 | 0,301 | 2,539 | 0,602 | |
0,301 | 0,000 | 0,778 | 0,477 | 1,447 | |
1,176 | 0,477 | 1,230 | 0,000 | 0,699 | |
| T = 50 ○С | ||||
σ=2,20 МПа | σ=2,06 МПа | σ=1,94 МПа | σ=1,85 МПа | σ=1,46 МПа | |
lgԏ | 0,477 | 0,000 | 1,000 | 2,664 | 1,380 |
0,000 | 1,000 | 2,714 | 0,699 | 0,000 | |
0,000 | 0,301 | 3,091 | 2,606 | 1,301 | |
0,000 | 0,000 | 0,477 | 2,400 | 0,301 | |
0,000 | 0,903 | 0,477 | 0,903 | 0,699 | |
0,000 | 1,732 | 2,250 | 1,342 | 1,279 | |
0,000 | 0,845 | 0,954 | 3,302 | 1,146 | |
1,398 | 1,301 | 0,301 | 1,322 | 2,569 | |
Полученные экспериментальные данные (таблица 1) были проверены на наличие грубых погрешностей по критерию Граббса. Также были найдены доверительные интервалы полученных экспериментальных значений. Полученные результаты средних значений и границы доверительного интервала сведены в таблицу 2.
Таблица 2 - Значения десятичного логарифма времени [с] при заданных напряжениях и температурах после статистической обработки данных
Напряжение (σ), МПа | Среднее значение логарифма долговечности и границы доверительного интервала при температуре | ||||||||||
30 °C | 40 °C | 50 °C | |||||||||
Н** | Ср* | В*** | Н** | Ср* | В*** | Н** | Ср* | В*** | |||
2,51 | -0,285 | 0,135 | 0,555 | - | - | - | - | - | - | ||
2,46 | 0,166 | 0,953 | 1,740 | - | - | - | - | - | - | ||
2,45 | - | - | - | -0,023 | 0,515 | 1,053 | - | - | - | ||
2,40 | -0,144 | 0,484 | 1,112 | - | - | - | - | - | - | ||
2,35 | - | - | - | -0,172 | 0,529 | 1,229 |
|
|
| ||
2,30 | 0,830 | 1,668 | 2,507 | - | - | - | - | - | - | ||
2,24 | - | - | - | 0,035 | 0,832 | 1,628 | - | - | - | ||
2,22 | 1,236 | 2,215 | 3,194 | - | - | - | - | - | - | ||
2,20 | - | - | - | - | - | - | -0,325 | 0,068 | 0,461 | ||
2,17 | - | - | - | 0,793 | 1,595 | 2,397 | - | - | - | ||
2,09 | - | - | - | 0,773 | 1,622 | 2,470 | - | - | - | ||
2,06 | - | - | - | - | - | - | 0,102 | 0,760 | 1,419 | ||
1,94 | - | - | - | - | - | - | 0,528 | 1,408 | 22,88 | ||
1,85 | - | - | - | - | - | - | 1,088 | 1,905 | 2,722 | ||
1,76 | - | - | - | - | - | - | 0,343 | 1,084 | 1,826 | ||
Примечание: *Ср – средние значения величины десятичного логарифма времени в секундах; **Н – нижняя граница доверительного интервала; ***В – верхняя граница доверительного интервала
По приведенным в таблице 2 статически обработанным данным построен график в координатах «lgԏ – σ» (рисунок 2).
Из графика видно, что при исследуемых температурах зависимость долговечности (lgԏ) от напряжения (σ) подчиняется линейной зависимости, при этом температурные прямые сходятся в «прямой пучок», т.е. наблюдается схождение в полюс при предельно высокой температуре, что является классическим представлением термофлуктуационной теории для данного материала.
По графику (рисунок 2) можно определить, что точка полюса сходится по оси абсцисс σ = 2,75 МПа и по оси ординат lgԏ = - 1,38 с. Прямолинейная зависимость lgԏ = f(σ) при различных температурах описывается уравнениями, приведенными ниже:
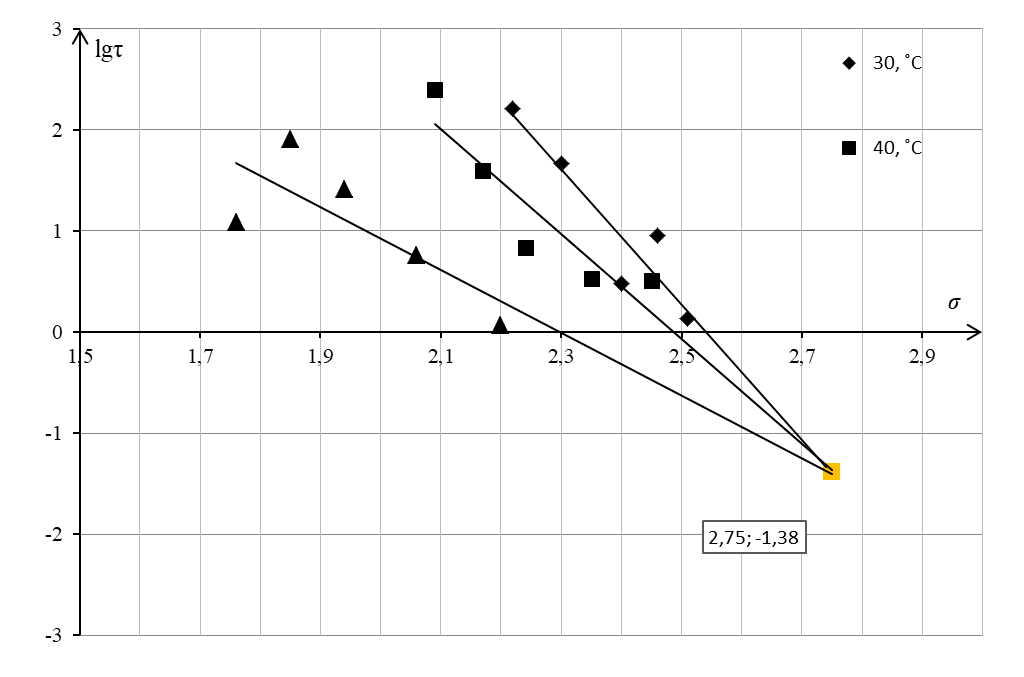
Рисунок 2 - Зависимость логарифма долговечности от напряжения для многослойных пластиковых сэндвич-панелей
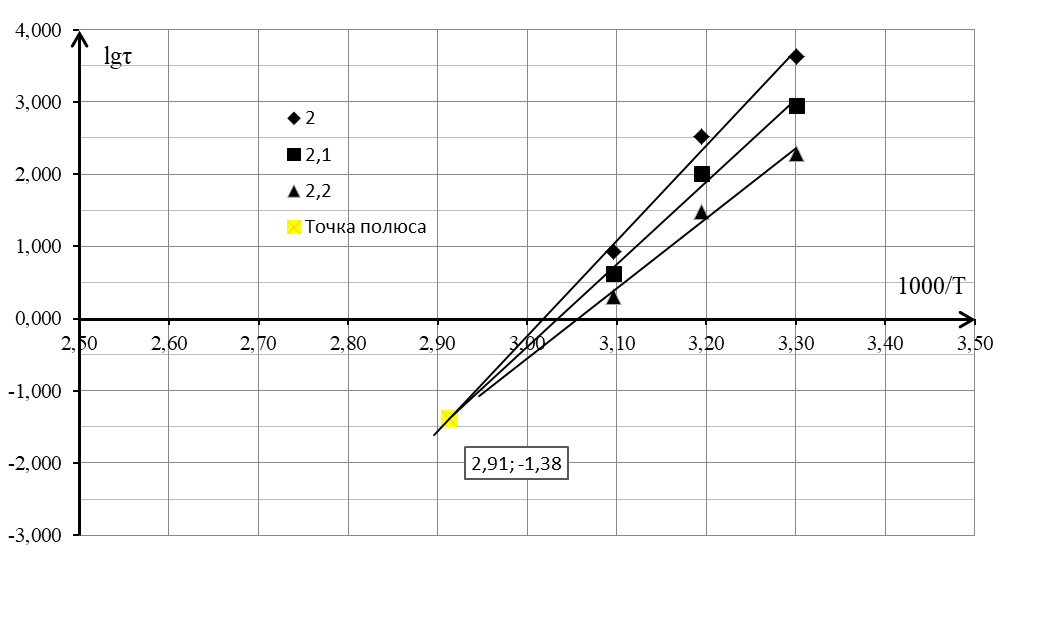
Рисунок 3 - Зависимость логарифма долговечности от обратной температуры увеличенной в 1000 раз для многослойных пластиковых сэндвич-панелей
Для каждой прямой графика «lgԏ – 1000/T», которая характеризует фиксированное значение напряжения, определялась энергия активации. Энергия активации для напряжения 2,0 МПа составляет U = 251,886 кДж/моль, для напряжения 2,1 МПа она составляет U = 218,244 кДж/моль и для напряжения 2,2 МПа – U = 184,603 кДж/моль. По найденным значениям строится прямая в координатах «U – σ» (рисунок 4). Данная прямая экстраполируется на ось ординат с целью определения начальной энергии активации. Таким образом, прямолинейная зависимость для образцов цельного сечения Uo = f(σ) описывается следующим уравнением:
Из данного уравнения определяются последние две константы Uo = 924,71 кДж/моль и ɣ = 336,41 кДж/(МПа×моль).
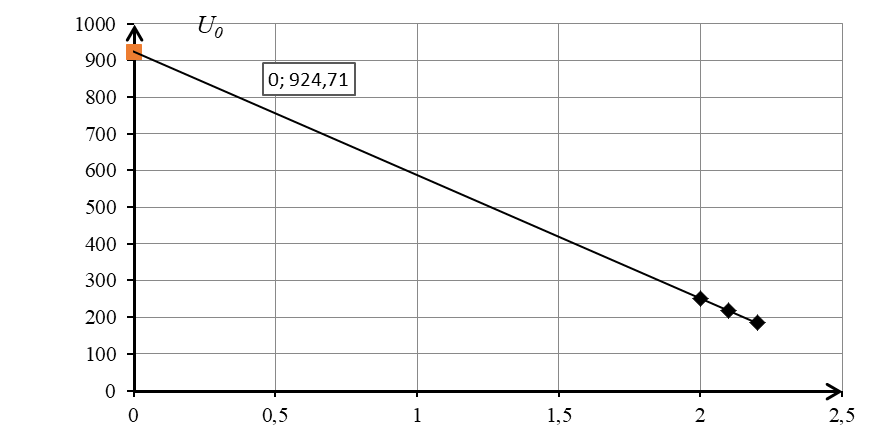
Рисунок 4 - Зависимость энергии активации процесса разрушения от напряжения для многослойных пластиковых сэндвич-панелей
Точка полюса (пересечение прямых температур (рисунок 2)) имеет координаты (2,75; -1,38). Следовательно, константа lgԏo, являющаяся ординатой точки полюса, равна -1,38.
Изменение угловых коэффициентов уравнения прямых температур (2), (3) и (4) описывается следующим уравнением:
тогда при a = 0, Tm = 343,24 К.
Согласно методу эталонного пучка, термофлуктуационная константа Uo определяется путем умножения значения эталонной константы на систему коэффициентов kσ и kk, а структурно-механическая константа ɣ определяется путем умножения эталонной константы на коэффициент kk.
Коэффициент kk = (-17,601)/(-2,619)=6,721, коэффициент kσ =2,75/10=0,275. Тогда U0 = 500∙6,721∙0,275=924,14 кДж/моль, а структурно-механическая константа ɣ = 50∙6,721=336,05 кДж/(МПа×моль).
4. Заключение
В итоге для многослойных пластиковых сэндвич-панелей классическим способом получены следующие термофлуктуационные константы обобщенного уравнения Журкова: lgԏ0 = -1,38 с, Tm = 343,64 К, U0 = 924,71 кДж/моль, ɣ = 336,41 кДж/(МПа×моль).
Для многослойных пластиковых сэндвич-панелей методом эталонного пучка получены следующие термофлуктуационные константы обобщенного уравнения Журкова: lgԏ0 = -1,38 с, Tm = 343,24 К, U0 = 924,14 кДж/моль, ɣ = 336,05 кДж/(МПа×моль).
Проведенные исследования на примере многослойных пластиковых сэндвич-панелей показали высокую сходимость двух методов определения термофлуктуационных констант обобщенного уравнения Журкова.
