ЭКСПЕРИМЕНТАЛЬНО-СТАТИСТИЧЕСКАЯ МОДЕЛЬ ИЗМЕНЕНИЯ ПРОЧНОСТИ ГИДРОТЕХНИЧЕСКИХ БЕТОНОВ ПРИ ИСПОЛЬЗОВАНИИ КОМПЛЕКСНЫХ МОДИФИЦИРУЮЩИХ ДОБАВОК
ЭКСПЕРИМЕНТАЛЬНО-СТАТИСТИЧЕСКАЯ МОДЕЛЬ ИЗМЕНЕНИЯ ПРОЧНОСТИ ГИДРОТЕХНИЧЕСКИХ БЕТОНОВ ПРИ ИСПОЛЬЗОВАНИИ КОМПЛЕКСНЫХ МОДИФИЦИРУЮЩИХ ДОБАВОК
Аннотация
В статье рассмотрен трехфакторный математический планируемый эксперимент. При вычислении зависимости от переменных факторов (Х1; Х2; Х3) для прочности при сжатии цементного камня в 28 суток использовался программный комплекс "PlanExp B-D13". Определены максимальные прочностные показатели полученных гидротехнических бетонов. Выполнена графическая интерпретация уравнения регрессии от действующих факторов. Значимость коэффициентов уравнений математической модели проверялась при помощи критерия Стьюдента. Адекватность уравнения математической модели проверялась с помощью критерия Фишера. Приемлемые значения варьируемых факторов определялись при помощи компромиссных значений с помощью анализа графических интерпретации уравнения регрессии, которое характеризует изменение значений предела прочности при сжатии в возрасте 28 суток.
Целью работы является оптимизация показателей прочности при сжатии гидротехнического бетона, модифицированного микрокремнеземом, с использованием добавки сульфоферритного типа.
1. Введение
Использование современных вычислительных математических программных комплексов в области анализа данных и построения регрессионных моделей позволяет оптимизировать процесс исследования и минимизировать затраты материальных и временных ресурсов, открывать возможности для автоматизации расчётов, обработки больших объёмов данных, строить различные типы регрессионных моделей, оценивать их качества, прогнозировать результаты и визуализировать полученные данные
, , , . Применение программных комплексов позволяет сократить материальные затраты на проведение экспериментов, уменьшить временные затраты на обработку данных, повысить точность результатов и упростить процесс анализа и интерпретации данных, что критически важно при работе со сложными системами, где необходимо учитывать множество переменных и проводить комплексный анализ для получения достоверных результатов .При оптимизации физико-механических параметров тяжелых гидротехнических бетонов используют определенные математические подходы, которые условно подразделяются на несколько групп:
1) вероятно-статистические методы, включающие использование общей теории вероятности, описательной статистики, выборочного метода и проверку статистических гипотез, дисперсного и регрессионного анализа, математической теории экспериментов и т.д.
;2) методы исследования операций, которые включают линейное, нелинейное и динамическое программирование, теорию игр, теорию массового обслуживания, теорию графов и сетей и т.п.
, ;3) методы математического анализа, включающие дифференциальное, интегральное и векторное исчисление, дифференциальные уравнения, в том числе уравнения математической физики, используемые для составления и расчета математических моделей на основе определенных предпосылок о физикохимии исследуемых процессов
;4) использование искусственного интеллекта
, , .В работе использовался трехфакторный планированный эксперимент . В качестве программно-алгоритмического средства обработки данных принят "PlanExp B-D13" . Данная программа обладает алгоритмом расчета, который включает в себя основные процедуры
, , :1) расчет коэффициентов функции отклика;
2) статистической обработка уравнений математической модели.
Основные вычисления, приведенные в работе, рассчитываются циклично, что может позволить перестроить уравнение математической модели моментально, при изменении параметров входных данных
, , .Целью работы является оптимизация показателей прочности при сжатии гидротехнического бетона, модифицированного микрокремнеземом, с использованием добавки сульфоферритного типа.
2. Основные результаты
В качестве участвующих в планировании эксперимента переменных факторов на 1 м3 тяжелого гидротехнического бетона принимаем:
• Х1 — портландцемент типа ЦЕМ I 42,5Н, выпускаемый АО «ЛИПЕЦКЦЕМЕНТ», кг.;
• Х2 — 10% микрокремнезем МК-85+ добавка сульфоферритного типа (изменяется от 12,5 до 17,5%) от массы портландцемента;
• Х3 — количество суперпластификатора для бетона BASF MasterGlenium ACE 430 – % от массы портландцемента;
Выходным параметром при планировании эксперимента выбран:
• Y1 — прочность на сжатие при выдерживании в нормальных условиях твердения в возрасте 28 суток, МПа.
Для получения результатов графической интерпретации использовался программный комплекс "Microsoft Excel".
В таблице 1 представлены факторы и интервалы их варьирования.
Таблица 1 - Факторы и интервалы их варьирования
Фактор | Нижний уровень (-1) | Основной уровень (0) | Верхний уровень (+1) | Интервал варьирования | Наименование фактора |
Х1: | 185 | 240 | 295 | 55 | Портландцемент типа ЦЕМ I 42,5Н, кг. |
Х2: | 22,5 | 25 | 27,5 | 2,5 | 10% микрокремнезем МК-85+ добавка сульфоферритного типа (изменяется от 12,5 до 17,5 %) от массы ПЦ |
Х3: | 1 | 1,5 | 2 | 0,5 | BASF MasterGlenium ACE 430, % от mц |
В таблице 2 план эксперимента и выходные параметры опытов.
Таблица 2 - План эксперимента и выходные параметры опытов
Номер опыта (u) | Матрица планирования | Натуральные значения переменных | Выходной параметр (Прочность в 28 суток, МПа) | ||||||
Х1 | Х2 | Х3 | Портландцемент типа ЦЕМ I 42,5Н, кг | 10% микрокремнезем МК-85 + добавка сульфоферритного типа (изменяется от 12,5 до 17,5 %) от mц | BASF MasterGlenium ACE 430, % от mц | y(u, 1) | y(u, 2) | y(u, 3) | |
1 | -1 | -1 | -1 | 185 | 22,5 | 1 | 56,1 | 45,8 | 47,6 |
2 | +1 | -1 | -1 | 295 | 22,5 | 1 | 40,0 | 43,1 | 53,5 |
3 | -1 | +1 | -1 | 185 | 27,5 | 1 | 46,7 | 43,8 | 61,7 |
4 | -1 | -1 | +1 | 185 | 22,5 | 2 | 52,8 | 61,6 | 57,0 |
5 | -1 | 0,19 | 0,19 | 185 | 25,5 | 1,6 | 65,3 | 64,9 | 64,6 |
6 | 0,19 | -1 | 0,19 | 250,5 | 22,5 | 1,6 | 55,0 | 48,7 | 58,0 |
7 | 0,19 | 0,19 | -1 | 250,5 | 25,5 | 1 | 51,9 | 53,2 | 60,1 |
8 | -0,29 | +1 | +1 | 224,1 | 27,5 | 2 | 49,6 | 53,7 | 52,2 |
9 | +1 | -0,29 | +1 | 295 | 24,3 | 2 | 62,6 | 68,5 | 59,5 |
10 | +1 | +1 | -0,29 | 295 | 27,5 | 1,4 | 52,9 | 46,3 | 54,3 |
Коэффициенты уравнения математической модели представлены в таблице 3.
Таблица 3 - Коэффициенты уравнения математической модели
b0 | b1 | b2 | b3 | b11 | b12 | b13 | b22 | b23 | b33 | |
Rсж.28 | 61,914 | -1,447 | -0,75 | 3,326 | 1,677 | -0,099 | 0,796 | -9,371 | -1,113 | -2,89 |
Значимость коэффициентов уравнений математической модели проверяется при помощи критерия Стьюдента (табл. 4). Адекватность уравнения математической модели проверяется по критерию Фишера.
Таблица 4 - Критерии Стьюдента и значимость коэффициентов математической модели
b0 | b1 | b2 | b3 | b11 | b12 | b13 | b22 | b23 | b33 | |
t-критерий | 12,616 | 0,689 | 0,357 | 1,583 | 0,413 | 0,04 | 0,318 | 2,308 | 0,444 | 0,712 |
Значимость | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
Примечание: 1/0 – значимый/незначимый
Дисперсия адекватности математической модели: 54,188.
Число степеней свободы при значимых коэффициентах: 8.
Табличное значение критерия Фишера: 2,45.
Расчетное значение критерия Фишера: 1,95.
Зависимость от переменных факторов (Х1; Х2; Х3) для прочности при сжатии цементного камня в 28 суток:
Зависимость переменных факторов для прочности показывает, что присутствие знаков «минус» при факторах Х1; Х2 и Х3 приводит к понижению прочности гидротехнического бетона. Положительная зависимость факторов Х1 и Х3 показывает повышение прочности при сжатии с единовременным увеличением вводимого суперпластификатора "BASF MasterGlenium ACE 430", что приводит к увеличению прочности гидротехнического бетона при сжатии.
В связи с тем, что для графической интерпретации функции трех переменных требуется четырехмерное пространство, поэтому для упрощения работы, а также удобством в будущем с уравнениями регрессии, функцию трех переменных требуется перевести в функцию двух переменных, при этом каждый раз принимая в виде константы один из используемых факторов. Основываясь на результатах уравнения регрессии для прочности при сжатии на 28-й день выдержки образцов в нормальных условиях, с использованием программного обеспечения "Microsoft Excel" были созданы графические представления уравнения регрессии, отражающего взаимосвязь между пределом прочности при сжатии и возрастом образцов (рис. 1–3). Каждый фактор, участвующий в построении графиков, фиксировался на нулевом уровне. Приемлемые значения варьируемых факторов определялись при помощи поиска компромиссных значений с помощью анализа графических интерпретации уравнения регрессии, характеризующего изменение предела прочности при сжатии в возрасте 28 суток.
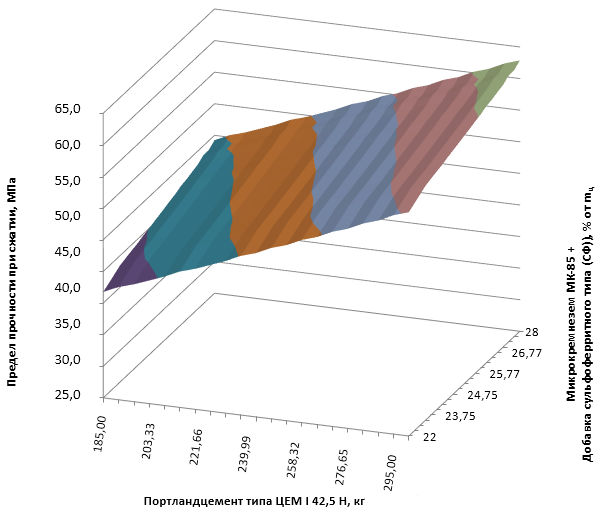
Рисунок 1 - Графическая интерпретация уравнения регрессии, характеризующего изменение предела прочности при сжатии в возрасте 28 суток от действующих факторов (Х1; Х2)
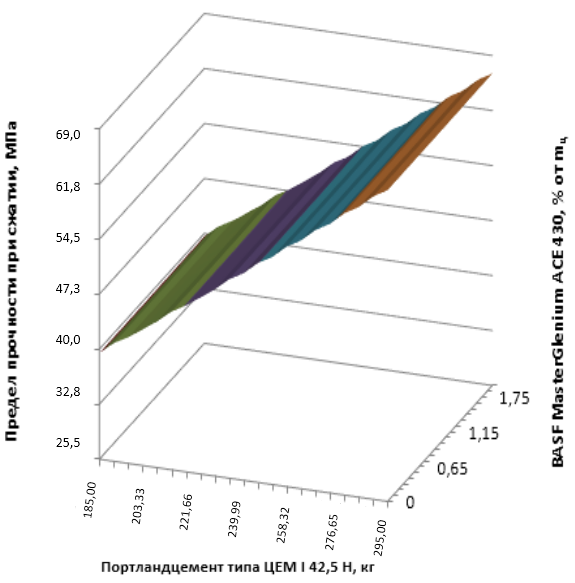
Рисунок 2 - Графическая интерпретация уравнения регрессии, характеризующего изменение предела прочности при сжатии в возрасте 28 суток от действующих факторов (Х1, Х3)

Рисунок 3 - Графическая интерпретация уравнения регрессии, характеризующего изменение предела прочности при сжатии в возрасте 28 суток от действующих факторов (Х2; Х3)
3. Заключение
По результатам проведенного математического планированного эксперимента, установлено, что требуемые показатели предела прочности при сжатии гидротехнических бетонов достигаются с использованием портландцемента типа ЦЕМ I 42,5Н в количестве 240 кг., 10% микрокремнезем МК-85 + добавка сульфоферритного типа 11% от массы портландцемента, суперпластификатора "BASF MasterGlenium ACE 430" 1,5% от массы цемента.
