МЕТОДИЧЕСКИЕ АСПЕКТЫ ОЦЕНКИ ВЛАЖНОСТНОГО РЕЖИМА НАРУЖНЫХ ОГРАЖДЕНИЙ
МЕТОДИЧЕСКИЕ АСПЕКТЫ ОЦЕНКИ ВЛАЖНОСТНОГО РЕЖИМА НАРУЖНЫХ ОГРАЖДЕНИЙ
Аннотация
Рассмотрена методическая проблема определения температуры в плоскости максимального увлажнения наружного ограждения при оценке влажностного режима здания из-за дискретного характера табличных данных, согласно своду правил СП 50.13330.2024. Целью данной работы является поиск обратной функции tм.у.(f) зависимости температуры в плоскости максимального увлажнения от значения комплекса f(tм.у.). Используя метод линеаризации найден линейный функционал комплекса f(tм.у.) и предложены две функции аппроксимации зависимости комплекса f(tм.у.) от температуры из которых получены расчетные формулы для определения температуры с заданной точностью. Дана оценка погрешности аппроксимации. Приведен пример расчета влажностного режима наружной стены на основе предложенного подхода. Результаты исследования дополняют методику оценки влажностного режима ограждающих конструкций и могут быть использованы при проектировании тепловой защиты зданий.
1. Введение
Согласно новой Энергетической стратегии РФ одним из ключевых направлений в строительной сфере является актуализация сводов правил, регулирующих проектирование инженерных систем теплоснабжения для поддержания комфортного микроклимата жилых и производственных зданий . Требования к улучшению надёжности и эффективности данных систем обуславливают актуальность задачи совершенствования методики проектирования тепловой защиты зданий.
Комфортные и допустимые значения параметров микроклимата определены в строительных нормах и санитарных нормах и правилах , . На микроклимат жилых помещений оказывают влияние такие факторы, как географическое положение здания, погодные условия, инсоляция, теплопотери через наружные ограждения, а также наличие источников тепловыделений внутри помещений. Согласно проектной документации, теплозащита и энергоэффективность зданий обеспечиваются за счет проведения теплотехнических расчетов ограждающих конструкций. Наряду с этим, в процессе проектирования обязательно оценивается влажностный режим этих конструкций, чтобы не допустить их переувлажнения, следуя методике, представленной в разделе 8 .
Главной особенностью обновленной редакции свода правил о тепловой защите зданий являются методические усовершенствования. Они нацелены на детализацию ключевых аспектов и снятие противоречий в расчетной методике. Так, например, в старой версии методики (СНиП 23-02-2003) парциальное давление насыщенного водяного пара E (Па) оценивается по температуре в плоскости возможной конденсации влаги внутри наружного ограждения (ПМУ), без указания на источник, в качестве которого можно было бы сослаться на Приложение С или Приложение 3 , где приведена исходная таблица давления E (мм.рт.ст.) со ссылкой на зарубежный первоисточник 1923 года. Табличные значения приведены для температур от -45 до +50 °C с точностью до десятых долей градуса. В актуальной версии нормативного документа предложена формула (8.9) для расчета данного показателя, которая обеспечивает хорошую аппроксимацию табличных данных в смысле минимума среднеквадратической ошибки (СКО).
Обновленный свод правил СП 50.13330.2024 также регламентирует методику определения зоны конденсации влаги в наружном ограждении. Методика предполагает расчет комплекса f(tм.у.) по формуле:
Значения функции комплекса рассчитываются с учетом климатических и конструкционных параметров, описание которых приведено в первоисточнике , формула (8.7).
Температура ПМУ для каждого слоя устанавливается по таблице 12 в соответствии с полученными значениями fi(tм.у.).
Однако здесь возникает практическая трудность из-за методической недоработки, поскольку на практике расчетные значения комплекса редко попадают в табличные данные, а кроме того, значения температур приведены с округлением до целого, тогда как при построении температурного профиля в поперечном сечении конструкции ограждения необходимо обеспечить точность расчетов до десятых долей. Данная проблема не решается и при использовании «упрощенного» метода определения плоскости ПМУ, изложенного в разделе 8.3 . В первом приближении можно использовать метод линейной интерполяции для определения температуры tм.у. по двум соседним точкам данных таблицы 1.
Таблица 1 - Зависимость комплекса f(tму) от температуры в плоскости максимального увлажнения
tму, °C | f(tму), K2/Па | tму, °C | f(tму), K2/Па | tму, °C | f(tму), K2/Па | tму, °C | f(tму), K2/Па |
-40 | 2539 | -23 | 616,9 | -6 | 181,1 | 11 | 62,0 |
-39 | 2322 | -22 | 571,2 | -5 | 169,3 | 12 | 58,5 |
-38 | 2126 | -21 | 529,2 | -4 | 158,4 | 13 | 55,2 |
-37 | 1947 | -20 | 490,7 | -3 | 148,3 | 14 | 52,1 |
-36 | 1785 | -19 | 455,2 | -2 | 138,9 | 15 | 49,1 |
-35 | 1638 | -18 | 422,5 | -1 | 130,2 | 16 | 46,4 |
-34 | 1504 | -17 | 392,5 | 0 | 122,1 | 17 | 43,9 |
-33 | 1382 | -16 | 364,8 | 1 | 114,5 | 18 | 41,5 |
-32 | 1271 | -15 | 339,2 | 2 | 107,5 | 19 | 39,2 |
-31 | 1170 | -14 | 315,6 | 3 | 100,9 | 20 | 37,1 |
-30 | 1077 | -13 | 293,9 | 4 | 94,8 | 21 | 35,1 |
-29 | 992,7 | -12 | 273,8 | 5 | 89,1 | 22 | 33,2 |
-28 | 915,5 | -11 | 255,2 | 6 | 83,8 | 23 | 31,5 |
-27 | 844,8 | -10 | 238,0 | 7 | 78,8 | 24 | 29,8 |
-26 | 780,2 | -9 | 222,1 | 8 | 74,2 | 25 | 28,3 |
-25 | 721,0 | -8 | 207,4 | 9 | 69,9 | 26 | 26,8 |
-24 | 666,7 | -7 | 193,7 | 10 | 65,8 | 27 | 25,4 |
Примечание: источник [4], таблица 12
Данная работа направлена на поиск обратной функции tм.у.(f), которая свяжет значение комплекса f(tм.у.), с искомой температурой. Решение этой задачи устранит отмеченный выше методический пробел. Для определения обратной функции применимы аналитические методы, а также приближенные, основанные на аппроксимации табличных данных с помощью специализированных алгоритмов , .
2. Методы и принципы исследования
Используя метод линеаризации нелинейной зависимости комплекса f(tм.у.), определим функционал комплекса
где T = tм.у. + 273 — температура в Кельвинах.
СКО аппроксимации линейной зависимости функционала составила 7,93·10-4, что говорит о хорошем приближении. Следовательно, эмпирическая функция аппроксимации комплекса f(tм.у.) в зависимости от температуры tм.у. имеет вид:
где tм.у. — температура, °С;
Тогда из формулы (4) можно выразить и определить температуру в плоскости ПМУ, tм.у., °C с заданной точностью (например, до десятых долей) по формуле:
Решение задачи линеаризации зависимости f(tм.у.) методом наименьших квадратов с нормированием результатов расчета позволило найти формулу, обеспечивающую бо́льшую точность расчета:
В этом случае искомую температуру можно найти по формуле:
3. Основные результаты
Математическое моделирование зависимости комплекса f(tм.у.) и его функционала F от температуры tм.у(°С), вычисленных по формулам (4) и (3) соответственно, выполнено в программе Маткад (см. рис. 1).
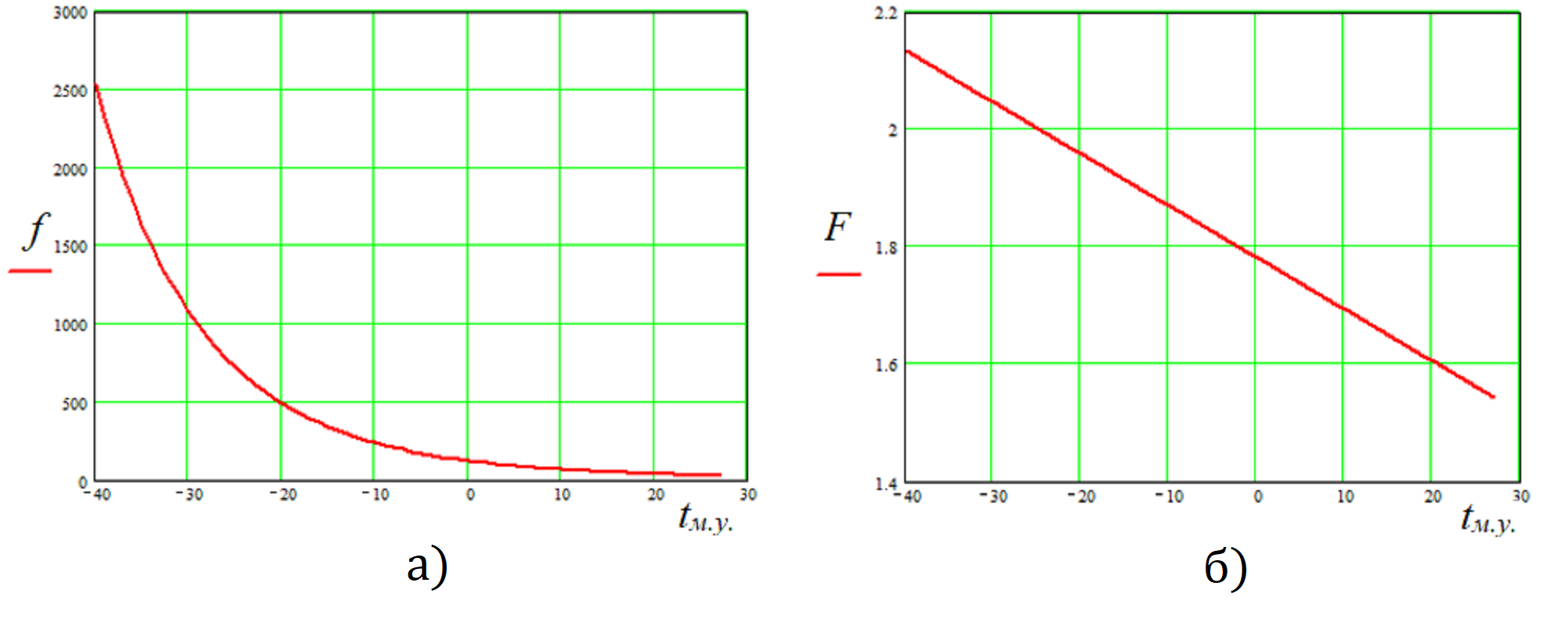
Рисунок 1 - Результаты аппроксимации температуры в плоскости максимального увлажнения:
а) зависимость комплекса f(tм.у.); б) линейный функционал F
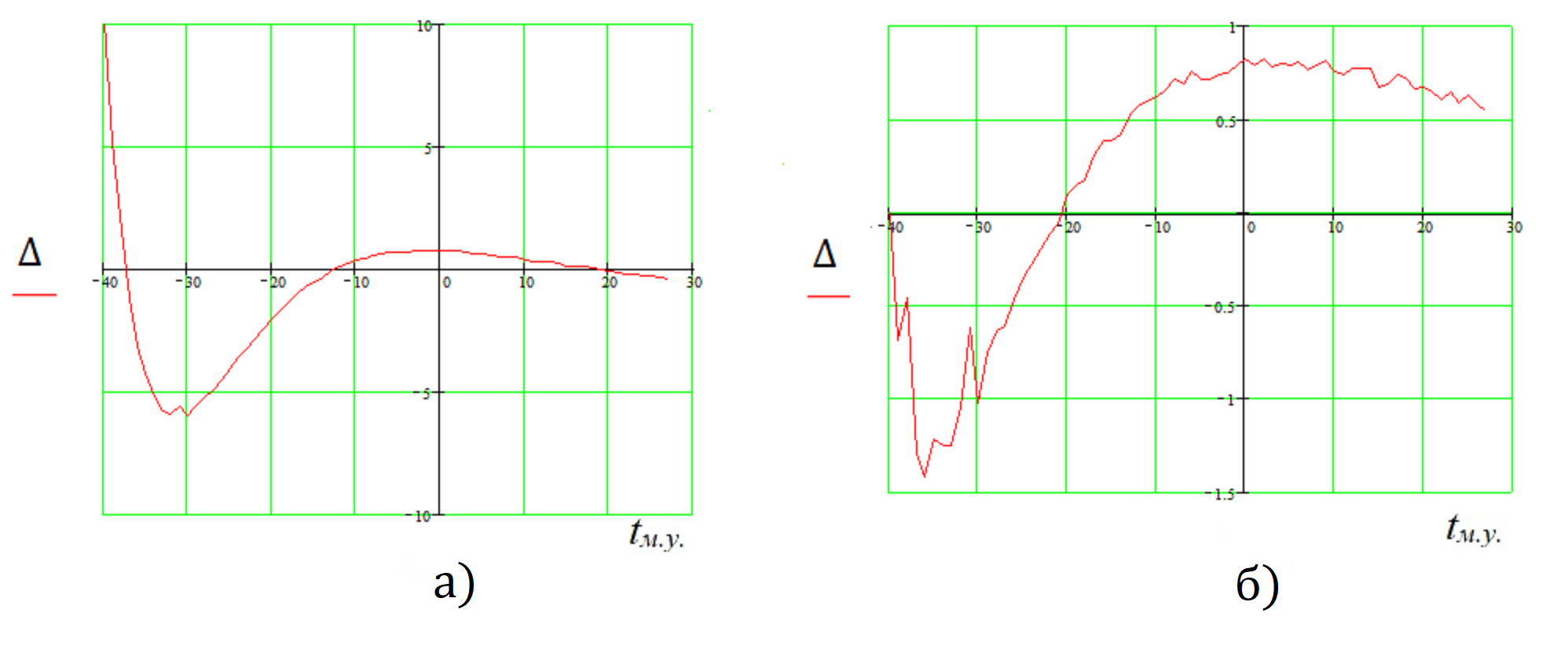
Рисунок 2 - Абсолютная ошибка ∆ аппроксимации зависимости f(tм.у.):
а) по формуле (4); б) по формуле (6)
Как видно из рисунка наибольшие отклонения расчетных значений от табличных проявляются при больших значениях комплекса для отрицательных температур. Заметим, что абсолютная ошибка носит регулярный характер, что можно было бы учесть в математической модели для повышения точности аппроксимации. Например, для компенсации ошибки в формулу (4) можно ввести дополнительное слагаемое Err в виде:
Это позволит уменьшить ошибку аппроксимации СКО в 4 раза. Однако, с практической точки зрения такой незначительной ошибкой можно пренебречь, поскольку решается обратная задача оценки аргумента функциональной зависимости f(tм.у.).
Расчет по формуле (6) позволяет уменьшить СКО ошибку аппроксимации в 15 раз по сравнению с формулой (4).
При округлении результатов расчета по формулам (5) или (7) до целых значений получим значения температур, полностью совпадающие с данными таблицы 1.
С учетом найденных функциональных зависимостей предлагается дополнить методику оценки влажностного режима наружных ограждений согласно разделу 8 свода правил
. В таком случае, алгоритм оценки будет содержать следующие этапы:1) расчет комплекса f(tм.у.) по формуле (2) для каждого слоя многослойного наружного ограждения по их заданным характеристикам для средней температуры за период влагонакопления согласно п. 8.5.1 методики ;
2) взамен приближенной ручной оценки температуры в плоскости максимального увлажнения по п. 8.5.2 свода правил предлагается расчет температуры tм.у. с требуемой точностью по формуле (5) или (7), предложенным в данном исследовании.
3) дальнейший анализ результатов расчета проводится в соответствии с п. 8.5.3 – п. 8.5.5 методики.
Приведем пример оценки места расположения ПМУ в сечении наружной стены с использованием предлагаемого в работе подхода. Климатические данные района проектирования, город Муром Владимирская обл., взяты по данным строительной климатологии . Характеристика материалов конструкции наружной стены приведена в таблице 2.
Таблица 2 - Характеристика материалов слоёв конструкции наружной стены
Материал слоя | Толщина δ, м | Коэффициент теплопроводности λ, Вт/(м·°C) | Коэффициент паропроницаемости μ, мг/(м·ч·Па) |
1 – штукатурка цементно-песчаная | 0,01 | 0,93 | 0,09 |
2 – кирпич силикатный | 0,38 | 0,87 | 0,11 |
3 – утеплитель (пенополистирол) | 0,10 | 0,04 | 0,05 |
4 – кирпич облицовочный | 0,12 | 0,52 | 0,16 |
Для указанной конструкции наружной стены рассчитаны теплотехнические показатели:
– фактическое сопротивление теплопередаче
– расчетное сопротивление паропроницанию Rп = 6,287 м2 ·Па·ч / мг.
Расчет выполнен в программе Маткад (см. рисунок 3). Данные расчета комплекса fi(tм.у.), температур tм.у. в сечении наружной стены приведены в таблице 3.
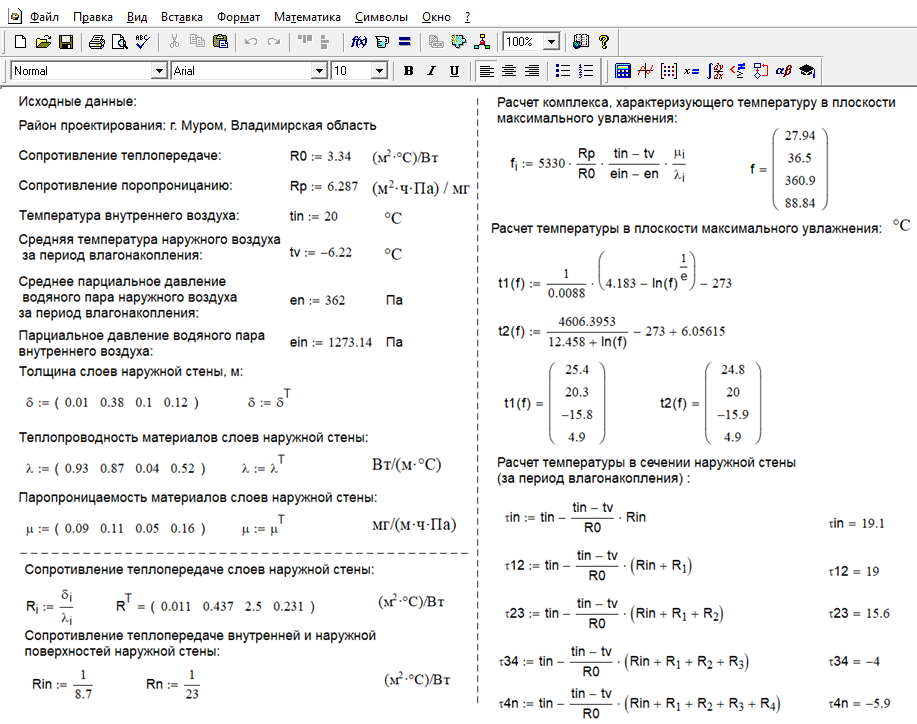
Рисунок 3 - Расчет влажностного режима наружной стены в программе Маткад
Таблица 3 - Результаты расчета
№ слоя | Значение комплекса fi(tм.у.) | Температура tм.у., °C по (5) | Температура tм.у., °C по (7) | Температура на границе слоёв, °C |
Внутренняя поверхность | – | – | – | 19,1 |
слой 1 | 27,94 | 25,4 | 24,8 | 19 |
слой 2 | 36,5 | 20,3 | 19,9 | 15,6 |
слой 3 | 360,9 | -15,8 | -15,9 | -4 |
слой 4 | 88,84 | 4,9 | 4,9 | -5,6 |
Значения температур на границах слоев рассчитаны по методике (формула (8.12)) для средней температуры периода влагонакопления tн.отр = -6,2°C. По результатам расчетов построен температурный профиль в сечении наружной стены (см. рис. 4).
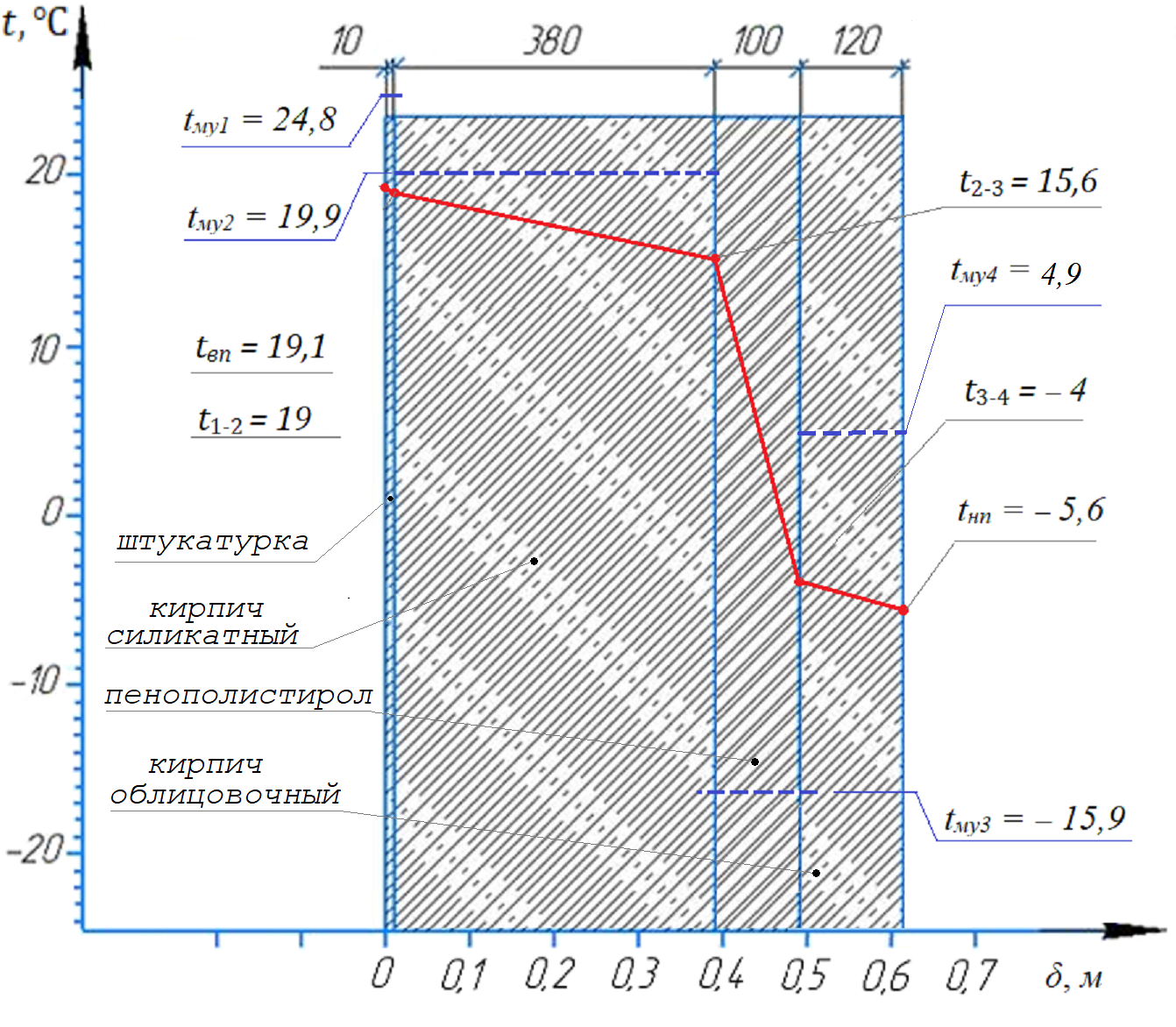
Рисунок 4 - Температурный профиль в сечении наружной стены
4. Заключение
В данном исследовании был проведен анализ методики оценки влажностного режима наружных ограждений зданий и рассмотрена методическая проблема определения температуры в плоскости максимального увлажнения из-за дискретного характера табличных данных, согласно своду правил СП 50.13330.2024. Предложены формулы для расчета температуры в сечении наружного ограждения здания с требуемой точностью. Результаты исследования дополняют методику оценки влажностного режима ограждающих конструкций и могут быть использованы при проектировании тепловой защиты зданий.
