Совершенствование метода расчета сдвиговой осадки буронабивных свай
Совершенствование метода расчета сдвиговой осадки буронабивных свай
Аннотация
В рамках исследования совершенствуется метод расчета сдвиговой осадки буронабивных свай. В результате анализа состояния установлено, что сдвиговая осадка используется как один из основных параметров в нескольких методах расчета свай и свайных фундаментов. При этом само значение сдвиговой осадки в большинстве случаев берется либо по табличным значениям (которые установлены для забивных свай), либо по результатам дорогостоящих полевых испытаний. На сегодняшний день отсутствует общепринятый аналитический метод расчета сдвиговой осадки, позволяющий устанавливать ее значения на этапе проектирования. Предлагаемый метод расчета основан на решении задачи теории упругости в плоской постановке. Аналитическая модель представляет собой вытянутый вдоль вертикальной оси вырез эллиптической формы. Решение задачи выполняется относительно перемещений выреза в линейно деформируемом полупространстве. Для решения модель отображается на конформно вспомогательную полуплоскость через функции отображения. В результате решения второй основной задачи теории упругости были получены функции напряжений и уравнения для определения главных и касательных напряжений на границах выреза при его перемещении. Для определения сдвиговой осадки полученные в ходе решения уравнения касательные напряжения на границах контура приравниваются к эпюре распределения сопротивления по боковой поверхности. Перемещение контура, при котором все значения максимальных касательных напряжений окажутся больше либо равны сопротивлению сваи по боковой поверхности (по всей ее длине), будет соответствовать сдвиговой осадке. Представленный метод расчета был апробирован на объекте по ул. Таврической в г. Сочи. Фундамент проектируемого здания был выполнен из буровых свай длиной 23,5 м и диаметром 0,63 м. В результате расчета сдвиговая осадка сваи составила 1,22 мм. В результате верификационного расчета по графоаналитическому методу, предложенному Б.И. Далматовым (1975), была получена удовлетворительная сходимость результатов.
1. Введение
Согласно данным последних исследований, в диапазоне эксплуатационных нагрузок можно выделить два основных участка. Первый участок начинается с момента приложения нагрузки на сваю и характеризуется активным включением ее боковой поверхности. После достижения определенного перемещения сваи сопротивление по боковой поверхности достигает предельного значения, и вся дальнейшая нагрузка приходится на ее нижний конец. Осадка, соответствующая данному перемещению, является сдвиговой
. Учитывая, что в пределах эксплуатационных нагрузок осадка сваи может оказаться как в пределах до сдвиговой (например, для длинных свай, как это приводится в источнике ), так превышающей ее, многими авторами выделяются различные методы расчета на данных участках , . Соответственно, корректное определение сдвиговой осадки на этапе проектирования фундамента позволяет избежать ошибок в выборе метода расчета конечной осадки зданий и сооружений. Также установлено, что при осадке сваи меньше сдвиговой практически нивелируется ее приращение в ходе нескольких циклов нагружения и разгрузки .Согласно исследованиям, проводимым Ф.К. Лапшиным и Б.И. Далматовым, значения сдвиговой осадки забивных свай колеблются в зависимости от вида грунта в пределах 5−25 мм
. Кроме того, авторами была разработана графоаналитическая методика определения сдвиговой осадки забивных свай по результатам статических испытаний. Методика заключается в логарифмировании зависимости «осадка сваи – приложенная сила» и последующем определении пересечения двух прямых линий, характеризующих работу сваи до и после сдвиговой осадки . Также существует инженерный метод определения нагрузки на буронабивную сваю, соответствующей ее сдвиговой осадке, описанный в источнике . Данный метод основан на разбиении осадки сваи в пределах эксплуатационных нагрузок на два участка – до и после сдвиговой осадки. Перемещения сваи на первом участке описываются формулой, предложенной В.Г. Федоровским , а на втором – формулой Шлейхера для круглого штампа. Осадка, соответствующая точке пересечения двух прямых, является сдвиговой. Основным недостатком данного метода можно считать необходимость проведения штамповых испытаний в уровне нижнего конца свай, что представляется трудоемким и технически сложным процессом. Также следует отметить инженерный метод определения сдвиговой осадки, основанный на результатах обработки около 50 буронабивных свай .Основные существующие методики определения сдвиговой осадки основаны либо на эмпирических данных, либо на основе результатов специфических и дорогостоящих испытаний. В случае необходимости определения значений сдвиговой осадки в процессе проектирования фундаментов приходится руководствоваться табличными данными, которые не всегда соответствуют действительности, так как не учитывают геометрические характеристики свай и неоднородность грунтов вдоль боковой поверхности. Зависимость сдвиговой осадки от геометрических размеров сваи установлена для глинистых грунтов в ходе численных исследований .
2. Основные результаты
Предлагаемая методика основана на решении плоской задачи теории упругости. Свая представляется в виде вытянутого в вертикальном направлении выреза со сглаженным концом при x = 0 и y = ix. Расчетная схема задачи приведена на рис. 1.
Зададим точкам выреза одинаковое перемещение вдоль оси
Отобразим конформно вспомогательную полуплоскость без выреза при η ≥ 0 (Рис. 1б) на заданную полуплоскость с вырезом следующей функцией :
Представим соответствие точек при конформном отображении:
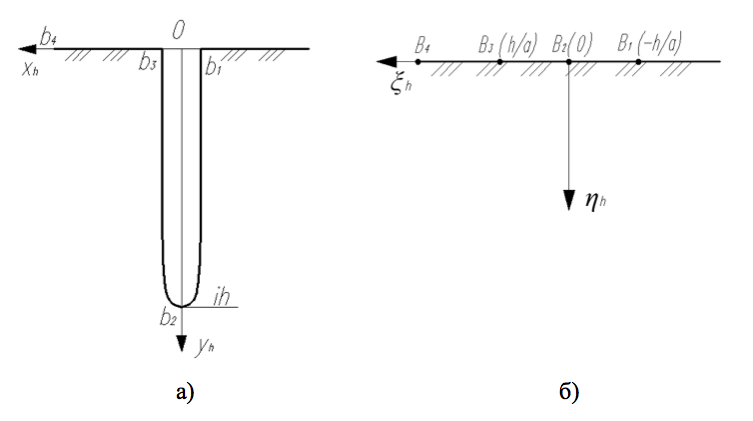
Рисунок 1 - Расчетная схема
Примечание: а) расчетная область; б) вспомогательная полуплоскость
Формулу (2) заменим на формулу (4) в параметрическом виде и в относительных координатах:
Формулу (3) заменим формулой (5):
Для упрощения записи заменим в (4) и (5) абсолютные координаты на относительные:
т. е. на границе области имеем:
Для решения второй основной задачи теории упругости необходимо определить функции напряжений и
, удовлетворяющие дифференциальному уравнению :
где ;
– коэффициент Пуассона;
– модуль упругости;
g1 и g2 – перемещения вдоль осей Оx и Oy соответственно.
На границе вспомогательной полуплоскости – действительная переменная. Обозначим
. Для точек границы уравнение (6) примет вид:
Умножим обе части уравнения (7) на дробь и проинтегрируем его по Коши:
или
Выражение (8) стремится к нулю при .
Сопряженное к (7) уравнение имеет вид:
где
Умножим обе части уравнения (9) на дробь и проинтегрируем его по Коши от
до
:
откуда
Выражение (12) стремится к нулю при
Вычисление напряжений на границах контура. Вычисления напряжений через вспомогательные координаты производится по формулам :
где
В заданных координатах (х;y):
Первое из уравнений (14) и (15) для при
примет вид:
Распишем слагаемые для второго уравнения из формулы (14):
где
где
Из формулы (3) проинтегрируем фрагмент с индексом «w»:
где
При имеем:
где
где
Теперь выпишем выражение для функции с подстановкой выражений из формулы (19):
где
Из второго уравнения в формуле (14) получаем после подстановок из формул (17), (18) и (21):
Откуда получаем, разделяя действительные и мнимые части, два уравнения:
Решая совместно уравнения (16) и (23), получаем значения и
, тангенциальные и нормальные к границе напряжения соответственно. По формуле (29) определяем касательные напряжения на контуре выреза.
Для определения сдвиговой осадки свай необходимо определить значения максимальных касательных напряжений, для этого необходимо перейти к главным напряжениям ( и
):
Значения нормальных напряжений , полученные по формулам (16) и (23), умноженные на коэффициент трения μ, необходимо сравнить со значениями расчетных сопротивлений по боковой поверхности, приведённым в таблице 7.3 СП 24.13330.2011 «Свайные фундаменты». Значения следует определять отдельно для каждого инженерно-геологического элемента и наносить на расчетную схему (в общем виде приведена на рис. 2). Далее следует последовательно увеличивать осадку сваи вплоть до достижения момента, когда значения эпюры (
) окажутся выше расчетных сопротивлений по всей длине боковой поверхности рассматриваемой сваи. Осадка сваи, соответствующая предельному равновесию теоретически полученных и предельно допустимых значений трения по боковой поверхности сваи, принимается за сдвиговую.
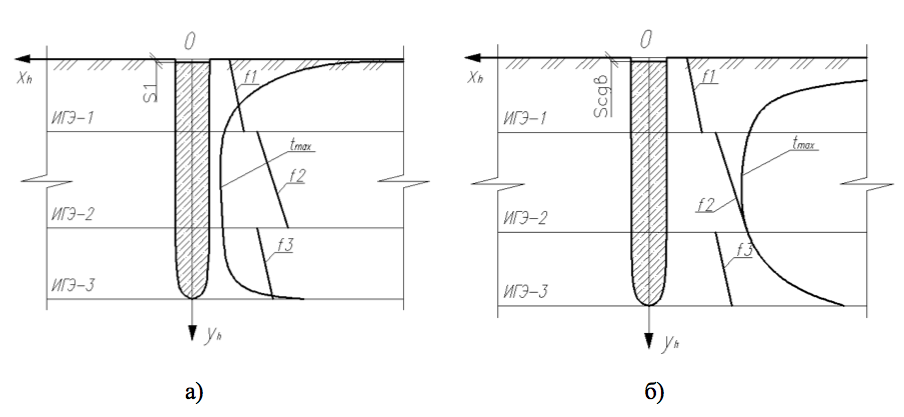
Рисунок 2 - Расчетная схема для определения сдвиговой осадки
Примечание: а) в начале нагружения; б) при достижении сдвиговой осадки
Предлагаемый метод использовался для расчета сдвиговой осадки буронабивных свай длиной 23,5 м и диаметром 0,63 м на площадке строительства многоэтажного жилого дома по ул. Таврической в г. Сочи Краснодарского края. Грунтовые условия рассматриваемой площадки приведены в таблице 1. Приведем расчет сдвиговой осадки сваи № 2. Вначале необходимо построить эпюру распределения предельного сопротивления сваи по боковой поверхности. Для упрощения расчета все инженерно-геологические элементы располагаем горизонтально. Эпюра предельного сопротивления строится по таблице 7.3 СП «Свайные фундаменты».
Таблица 1 - Грунтовые условия опытной площадки по ул. Таврической в г. Сочи
Характеристика | Значение для грунтов | |||||
ИГЭ 2. Суглинок тяжелый тугопластичной консистенции, непросадочный, незасоленный, ненабухающий | ИГЭ 3. Глина легкая тугопластичной консистенции, непросадочная, незасоленная, ненабухающая | ИГЭ 4. Песок средней крупности, насыщенный водой | ИГЭ 5. Галичнековый грунт с супесчаным пластичным заполнителем, невыветрелый, очень прочный, насыщенный водой | ИГЭ 6. Супесь пластичная, непросадочная | ИГЭ 7. Глина тяжелая полутвердой консистенции, непросадочная, незасоленная, ненабухающая | |
Влажность в естественном состоянии, % | 27,5 | 33,4 | 24,2 | 20,7 | 18,1 | 27,7 |
Плотность грунта, г/см3 | 1,93 | 1,96 | 1,84 | 2,3 | 2,16 | 2,05 |
Коэффициент пористости | 0,78 | 0,9 | 0,91 | - | 0,45 | 0,7 |
Показатель текучести | 0,31 | 0,32 | - | 0,5 | 0,5 | 0,11 |
Угол внутреннего трения, град | 18 | 17 | 35 | 27 | 21 | 20 |
Удельное сцепление, кПа | 22 | 38 | 1 | 3 | 19 | 60 |
Модуль деформации, МПа | 6,7 | 4,6 | 32 | 35,6 | 10,1 | 9,8 |
Примечание: источник [12]
С учетом полученных значений эпюры сопротивления по боковой поверхности выполняется расчет максимальных касательных напряжений с заданными перемещениями. Для расчета используются средневзвешенные по длине сваи значения модуля деформации и коэффициента Пуассона грунтов основания. При расчете данных характеристик на площадке по ул. Виноградной средневзвешенное значение модуля деформации составило 18,04 МПа, коэффициента Пуассона 0,29. Первоначальные характеристики грунтов площадки приведены в Приложении. Перемещения сваи увеличиваются вплоть до превышения всех точек эпюры () относительно эпюры распределения значений трения по боковой поверхности fi. Точность расчета обеспечивается необходимым числом итераций. На рисунке 3 приведены эпюры распределения максимальных касательных напряжений при разной (в т. ч. сдвиговой) осадке. Полученное в расчете значение сдвиговой осадки составило 1,55 мм.
Для верификации полученного результата был использован графоаналитический метод, предложенный Б.И. Далматовым . Результаты статических испытаний сваи № 2 (рис. 4а) были преобразованы в логарифмической шкале для нахождения точки пересечения двух прямых, характеризующих работу сваи до и после сдвиговой осадки (рис. 4б). Осадка сваи, соответствующая точке пересечения двух прямых, является сдвиговой и составляет в данном случае 1,39 мм.
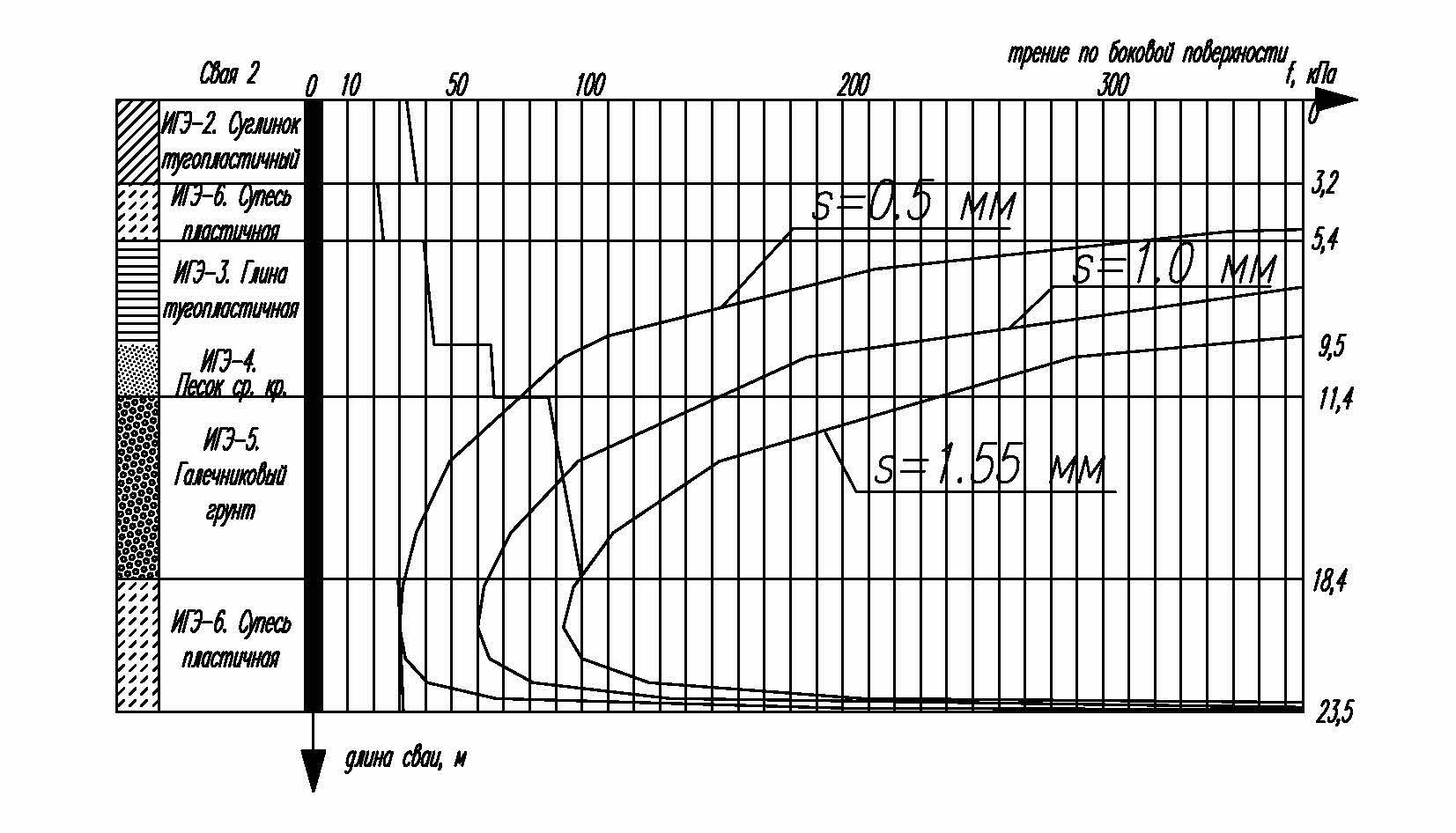
Рисунок 3 - Расчет сдвиговой осадки сваи
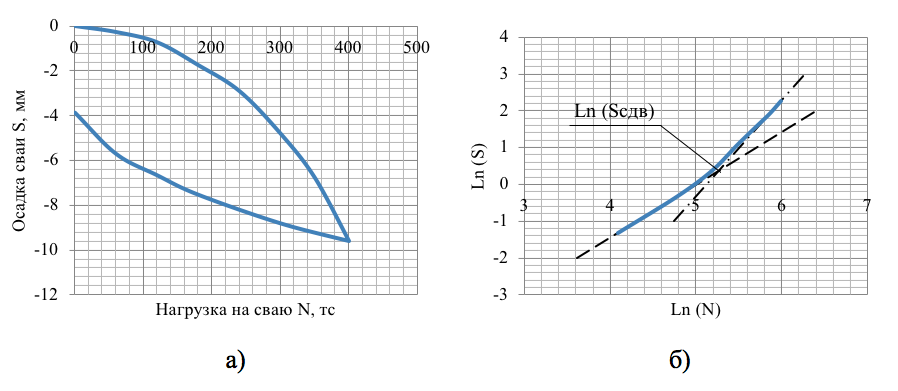
Рисунок 4 - Зависимость осадки сваи от приложенной нагрузки
Примечание: а) исходная зависимость; б) в логарифмической шкале
3. Заключение
Разработан метод, позволяющий оценивать значения сдвиговой осадки сваи в процессе ее нагружения.
Расхождение полученного аналитически значения сдвиговой осадки сваи с установленным в ходе статических испытаний составило 0,16 мм, что позволяет говорить об удовлетворительной сходимости результатов.
